题目内容
已知正数组成的等比数列{an},若a1•a20=100,那么a7+a14的最小值为( )
| A、20 | B、25 | C、50 | D、不存在 |
考点:等比数列的通项公式
专题:等差数列与等比数列
分析:由已知得a7+a14≥2
=2
=2
=20.
| a7a14 |
| a1a20 |
| 100 |
解答:
解:∵正数组成的等比数列{an},a1•a20=100,
∴a7+a14≥2
=2
=2
=20.
当且仅当a7=a14时,a7+a14取最小值20.
故选:A.
∴a7+a14≥2
| a7a14 |
| a1a20 |
| 100 |
当且仅当a7=a14时,a7+a14取最小值20.
故选:A.
点评:本题考查等比数列中两项和的最小值的求法,是基础题,解题时要认真审题,注意均值定理的合理运用.

练习册系列答案
相关题目
若函数f(x)在R上是单调递减的奇函数,则下列关系式成立的是( )
| A、f(3)<f(4) |
| B、f(3)<-f(-4) |
| C、-f(-3)<f(-4) |
| D、f(-3)>f(-4) |
若对实数a和b,定义运算“⊕”:a⊕b=(a+b)×(a-3b),则当x∈[1,8]时,(log2x)⊕1的最大值和最小值分别为( )
| A、-3,0 |
| B、0,-4 |
| C、-4,不存在 |
| D、-3,不存在 |
已知f(x)是偶函数,且在(-∞,0]上是增函数.若f(lnx)<f(1),则x的取值范围是( )
| A、(e,+∞) | ||
B、(
| ||
C、(e,+∞)∪(0,
| ||
D、(
|
已知:设命题p:实数x满足(x-a)(x-3a)<0,其中a>0.命题q:实数x满足
≤0.若¬p是¬q的
充分不必要条件,则实数a的取值范围.( )
| x-3 |
| x-2 |
充分不必要条件,则实数a的取值范围.( )
| A、(1,2] |
| B、[1,2] |
| C、(1,2) |
| D、(-∞,2] |
已知全集U={|x∈Z|1≤x≤6},集合A={1,2,3,4},B={2,4,6},则(∁UA)∩B=( )
| A、{6} |
| B、{2,4} |
| C、{2,4,6} |
| D、{1,2,3,4,6} |
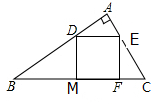 如图,正方形DEFM内接于△ABC,且点D,E在AB,AC上,点F,M在BC上,∠A=90°,S△CEF=1,S△BMD=4,求S△ABC.
如图,正方形DEFM内接于△ABC,且点D,E在AB,AC上,点F,M在BC上,∠A=90°,S△CEF=1,S△BMD=4,求S△ABC.