题目内容
设函数f(x)=logax(a>0,a≠1),
(1)若不等式f(x)-x2>0在(0,
)内恒成立,求a的取值范围;
(2)判断是否存在大于1的实数a,使得对任意x1∈[a,2a],都有x2∈[a,a2]满足等式:f(x1)+f(x2)=p,且满足该等式的常数p的取值唯一?若存在,求出所有符合条件的a的值;若不存在,请说明理由.
(1)若不等式f(x)-x2>0在(0,
| 1 |
| 2 |
(2)判断是否存在大于1的实数a,使得对任意x1∈[a,2a],都有x2∈[a,a2]满足等式:f(x1)+f(x2)=p,且满足该等式的常数p的取值唯一?若存在,求出所有符合条件的a的值;若不存在,请说明理由.
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:(1)将问题转化为在(0,
)内y=logax图象在y=x2图象的上方,得不等式组,解出即可;
(2)由题意得logax1+logax2=loga(x1x2)=p,把x2看作x1的函数x2=
,其在区间[a,2a]上单调递减,得不等式组,解出即可.
| 1 |
| 2 |
(2)由题意得logax1+logax2=loga(x1x2)=p,把x2看作x1的函数x2=
| ap |
| x1 |
解答:
解:(1)不等式logax>x2在(0,
)内恒成立,
所以在(0,
)内y=logax图象在y=x2图象的上方,
∴
,∴
≤a<1.
(2)假设存在大于1的实数a满足条件,
由f(x1)+f(x2)=p,即logax1+logax2=loga(x1x2)=p,
∴x1x2=ap,
把x2看作x1的函数x2=
,其在区间[a,2a]上单调递减,
∴x1∈[a,2a]时,x2∈[
,
],
∴
,∴
,
因为常数p的取值唯一,所以2+
=3,解得:a=2,
所以存在大于1的实数a,且a=2.
| 1 |
| 2 |
所以在(0,
| 1 |
| 2 |
∴
|
| 1 |
| 16 |
(2)假设存在大于1的实数a满足条件,
由f(x1)+f(x2)=p,即logax1+logax2=loga(x1x2)=p,
∴x1x2=ap,
把x2看作x1的函数x2=
| ap |
| x1 |
∴x1∈[a,2a]时,x2∈[
| ap |
| 2a |
| ap |
| a |
∴
|
|
因为常数p的取值唯一,所以2+
| log | 2 a |
所以存在大于1的实数a,且a=2.
点评:本题考查了对数函数的性质,考查了转化思想,是一道中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
| ∫ |
-
|
| A、1 | B、0 | C、-1 | D、2 |
函数f(x)=2sin(
-
)+1(x∈R)的最小正周期、最大值依次为( )
| x |
| 2 |
| π |
| 3 |
| A、4π,3 | B、4π,2 |
| C、2π,3 | D、2π,2 |
已知?的ABCD顶点A,B,C的坐标分别为(-2,1),(-1,3),(3,4),则顶点D的坐标为( )
| A、(4,6) |
| B、(2,2) |
| C、(0,0) |
| D、(0,4) |
已知f(x)是偶函数,且在(-∞,0]上是增函数.若f(lnx)<f(1),则x的取值范围是( )
| A、(e,+∞) | ||
B、(
| ||
C、(e,+∞)∪(0,
| ||
D、(
|
已知集合A={x|x2-2x-3≤0},B={x|y=1g
},则A∩B=( )
| 2-x |
| x+2 |
| A、[-1,2) |
| B、(-2,2) |
| C、(-1,3) |
| D、(2,3] |
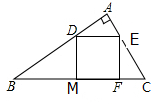 如图,正方形DEFM内接于△ABC,且点D,E在AB,AC上,点F,M在BC上,∠A=90°,S△CEF=1,S△BMD=4,求S△ABC.
如图,正方形DEFM内接于△ABC,且点D,E在AB,AC上,点F,M在BC上,∠A=90°,S△CEF=1,S△BMD=4,求S△ABC.