题目内容
已知函数f(x)=
,则满足不等式f(2x-3)>f(x)的x的取值范围为 .
|
考点:其他不等式的解法
专题:不等式的解法及应用
分析:由条件根据函数的单调性的性质可得
,或2x-3>x≥0,由此求得x的范围.
|
解答:
解:由函数f(x)=
,则满足不等式f(2x-3)>f(x),
可得
,或2x-3>x≥0,求得x>3,
故答案为:(3,+∞).
|
可得
|
故答案为:(3,+∞).
点评:本题主要求函数的单调性的性质,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
函数f(x)=2sin(2x+
)在区间(-π,π)上零点的个数为( )
| π |
| 3 |
| A、5 | B、4 | C、3 | D、2 |
若对实数a和b,定义运算“⊕”:a⊕b=(a+b)×(a-3b),则当x∈[1,8]时,(log2x)⊕1的最大值和最小值分别为( )
| A、-3,0 |
| B、0,-4 |
| C、-4,不存在 |
| D、-3,不存在 |
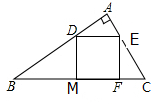 如图,正方形DEFM内接于△ABC,且点D,E在AB,AC上,点F,M在BC上,∠A=90°,S△CEF=1,S△BMD=4,求S△ABC.
如图,正方形DEFM内接于△ABC,且点D,E在AB,AC上,点F,M在BC上,∠A=90°,S△CEF=1,S△BMD=4,求S△ABC.