Question

已知函数f（x）=

|log3x|，0＜x＜3 1 3 x2- 10 3 x+8，x≥3

，关于x的方程f（x）=t有如下结论：
①任意实数t∈（-

1

3

，0），该方程都只有两根且两根之和为10；
②t=1是该方程有三个根的充分条件；
③该方程不可能只有一根；
④若该方程有四个根，则该四个根之和的范围是（12，

40

3

）．
其中正确结论的序号是

 

（填出所有正确结论的序号）．

Answer 1

考点：分段函数的应用

专题：数形结合,函数的性质及应用

分析：先配方求出函数的最小值，画出y=f（x）的图象和直线y=t，通过图象观察：直线的平移，与f（x）的交点的个数的变化，即可判断．

解答： 解：∵

1

3

x²-

10

3

x+8=

1

3

（x-5）²-

1

3

，
∴x=5时，取得最小值，且为-

1

3

．
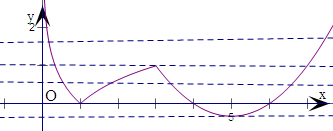
画出y=f（x）的图象和直线y=t，
由图象观察得到：
①当t∈（-

1

3

，0），方程f（x）=t都只有两根且两根之和为10，故①对；
②t=1时，该方程有三个根，故t=1是该方程有三个根的充分条件，故②对；
③t=-

1

3

时，该方程只有一个根，故③错；
④若该方程有四个根，由小到大设为x₁，x₂，x₃，x₄，则1+1+10＜x₁+x₂+x₃+x₄＜

1

3

+3+10，
即该四个根之和的范围是（12，

40

3

），故④对．
故答案为：①②④．

点评：本题考查分段函数的图象及应用，考查函数的最值和运用，同时考查数形结合的能力，属于中档题．