题目内容

已知球面上的点满足方程（x-1）2+（y+2）2+（z-3）2=9，点A（-3，2，5），则球面上的点与点A距离的最大值是
 
．
考点：空间中的点的坐标
专题：空间位置关系与距离
分析：由球面上的点满足方程（x-1）2+（y+2）2+（z-3）2=9，可得球心C（1，-2，3），半径r=3．利用两点之间的距离公式可得|CA|，即可得出球面上的点与点A距离的最大值=|CA|+r．
解答： 解：由球面上的点满足方程（x-1）2+（y+2）2+（z-3）2=9，可得球心C（1，-2，3），半径r=3．
∴|CA|=
(-3-1)2+(2+2)2+(5-3)2
=6．
则球面上的点与点A距离的最大值=|CA|+r=6+3=9．
故答案为：9．
点评：本题考查了球的方程、两点之间的距离公式，属于基础题．
练习册系列答案
相关题目
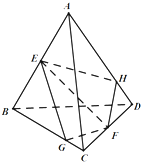如图，在四面体ABCD中，E，F分别为AB，CD的中点，过EF任作一个平面α分别与直线BC，AD相交于点G，H，则下列结论正确的是
 
．
①对于任意的平面α，都有直线GF，EH，BD相交于同一点；
②存在一个平面α0，使得GF∥EH∥BD；
③存在一个平面α0，使得点G在线段BC上，点H在线段AD的延长线上；
④对于任意的平面α，都有S△EFG=S△EFH．
已知函数f（x）=
|log3x|，0＜x＜3
1
3
x2-
10
3
x+8，x≥3
，关于x的方程f（x）=t有如下结论：
①任意实数t∈（-
1
3
，0），该方程都只有两根且两根之和为10；
②t=1是该方程有三个根的充分条件；
③该方程不可能只有一根；
④若该方程有四个根，则该四个根之和的范围是（12，
40
3
）．
其中正确结论的序号是
 
（填出所有正确结论的序号）．
已知a为非负数，若平面内三点A（-a，1），B（a2，2），C（a3，3）共线，则a=
 
．
有一堆形状、大小相同的珠子，其中只有一粒重量比其它的轻，某同学经过思考，他说根据科学的算法，利用天平，四次肯定能找到这粒最轻的珠子，则这堆珠子最多有
 
粒．
已知一列数1，1，2，3，5，…，根据其规律，下一个数应为
 
．
向量
a
，
b
的夹角大小为
3π
4
，且|
a
|=
2
，|
b
|=1，则
a
•（
a
+
b
）=
 
．
若2sinα+cosα=0，则
cosα+sinα
cosα-sinα
的值为（　　）
A、
2
3
B、-
2
3
C、
1
3
D、-
1
3
已知定义在R上的函数f（x）、g（x）满足f（x）=axg（x），f′（x）g（x）＜f（x）g′（x），其中g（x）≠0且
f(1)
g(1)
+
f(-1)
g(-1)
=
5
2
，在有穷数列{
f(n)
g(n)
}（n=1，2，3，…，10）中任取前k项相加，则前k项和大于
63
64
的概率是（　　）
A、
1
5
B、
3
5
C、
4
5
D、
2
5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网