题目内容
设n为正整数,由数列1,2,3,…n分别求相邻两项的和,得到一个有n-1项的新数列;1+2,2+3,3+4,…(n-1)+n即3,5,7,…2n-1.对这个新数列继续上述操作,这样得到一系列数列,最后一个数列只有一项.(1)记原数列为第一个数列,则第三个数列的第2项是 (2)最后一个数列的项是 .
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:首先用第二个数列的第2项加上第二个数列的第3项,求出第三个数列的第2项是多少即可;然后由题意可知最后一个数列的项an=2an-1+2n-2(n≥2,n∈N*),即
=
+
,即数列{
}是首项为
,公差为
的等差数列,进而求出最后一个数列的项即可.
| an |
| 2n |
| an-1 |
| 2n-1 |
| 1 |
| 4 |
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
解答:
解:第三个数列的第2项是:5+7=12;
由题意可知最后一个数列的项an=2an-1+2n-2(n≥2,n∈N*),
即
=
+
,
所以数列{
}是首项为
,公差为
的等差数列;
则
=
+
(n-1)=
,
所以an=(n+1)•2n-2(n∈N*),
即最后一个数列的项是 (n+1)•2n-2(n∈N*).
故答案为:12;(n+1)•2n-2(n∈N*).
由题意可知最后一个数列的项an=2an-1+2n-2(n≥2,n∈N*),
即
| an |
| 2n |
| an-1 |
| 2n-1 |
| 1 |
| 4 |
所以数列{
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
则
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| n+1 |
| 4 |
所以an=(n+1)•2n-2(n∈N*),
即最后一个数列的项是 (n+1)•2n-2(n∈N*).
故答案为:12;(n+1)•2n-2(n∈N*).
点评:本题主要考查了等差数列性质的运用,考查了构造法的运用,属于中档题,解答此题的关键是构造并判断出数列{
}是首项为
,公差为
的等差数列.
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
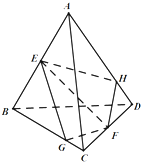 如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,则下列结论正确的是
如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,则下列结论正确的是