题目内容
设f(x)=x-ln|x|.
(1)判断函数f(x)的奇偶性,并说明理由;
(2)请用描点法画出函数f(x)的大致图象;
(2)设实常数a,b满足ab>0,试求f(x)在闭区间[a,b]上的最小值.
(1)判断函数f(x)的奇偶性,并说明理由;
(2)请用描点法画出函数f(x)的大致图象;
(2)设实常数a,b满足ab>0,试求f(x)在闭区间[a,b]上的最小值.
考点:函数的图象
专题:函数的性质及应用,导数的综合应用
分析:(1)先通过代特殊值验证f(x)的奇偶性,若具有奇偶性再用定义证明;
(2)易知f(x)非奇非偶,所以分x>0和x<0两种情况,先研究函数的性质,如单调性、坐标轴交点、极值等;
(3)根据第(2)问得到的单调性分a、b同正和同负两种情况讨论求值.
(2)易知f(x)非奇非偶,所以分x>0和x<0两种情况,先研究函数的性质,如单调性、坐标轴交点、极值等;
(3)根据第(2)问得到的单调性分a、b同正和同负两种情况讨论求值.
解答:
解:(1)∵f(e)=e-1,f(-e)=-e-1,显然,f(-e)≠f(e)且f(-e)≠-f(e),所以函数f(x)是非奇非偶函数;
(2)∵f(x)=x-ln|x|∴f(x)=
,
①当x>0时,f′(x)=1-
=
,当x∈(0,1),f′(x)<0,∴f(x)在(0,1)上递减;当x∈(1,+∞)时,f′(x)>0∴f(x)在(1,+∞)上递增;且当x→0时,lnx→-∞,所以x-lnx→+∞;当x→+∞时,∵x比lnx增长得快,∴x-lnx→+∞;x=1时取得最小值1.
②当x<0时,f′(x)=1-
>0恒成立,∴f(x)在(-∞,0)上递增;且x→-∞时,f(x)→-∞;当x→0时,f(x)→+∞.
∴f(x)=x-ln|x|的图象为

(3)∵ab>0,∴a<b<0或0<a<b,
①当a<b<0时,由(2)知f(x)在[a,b]上递增,∴ymin=f(a)=a-ln|a|;
②当0<a<b≤1时,由(2)知,f(x)在[a,b]上递减,∴ymin=f(b)=b-ln|b|;
③当0<a≤1<b时,f(x)在[a,1]上递减,在[1,b]上递增∴ymin=f(1)=1;
④当1≤a<b时,f(x)在[a,b]上递增,∴ymin=f(a)=a-lna
(2)∵f(x)=x-ln|x|∴f(x)=
|
①当x>0时,f′(x)=1-
| 1 |
| x |
| x-1 |
| x |
②当x<0时,f′(x)=1-
| 1 |
| x |
∴f(x)=x-ln|x|的图象为

(3)∵ab>0,∴a<b<0或0<a<b,
①当a<b<0时,由(2)知f(x)在[a,b]上递增,∴ymin=f(a)=a-ln|a|;
②当0<a<b≤1时,由(2)知,f(x)在[a,b]上递减,∴ymin=f(b)=b-ln|b|;
③当0<a≤1<b时,f(x)在[a,1]上递减,在[1,b]上递增∴ymin=f(1)=1;
④当1≤a<b时,f(x)在[a,b]上递增,∴ymin=f(a)=a-lna
点评:研究函数的性质一定要先看定义域,再根据函数奇偶性的定义(或图象)判断奇偶性,利用导数(或图象或定义)研究单调性;对于最值问题,主要还是利用单调性求最值,不能确定单调性的,要按照增减区间的分界点是否在区间内进行讨论;图象问题,还是看定义域、值域、单调性、极值等性质,然后画出简图.

练习册系列答案
相关题目
关于x的方程3x=a2+2a在(-∞,1]上有解,则实数a的取值范围是( )
| A、[-2,-1)∪(0,1] |
| B、[-3,-2)∪[0,1] |
| C、[-3,-2)∪(0,1] |
| D、[-2,-1)∪[0,1] |
 如图,PD⊥平面ABC,AC=BC,D为AB的中点,E为AP的中点.
如图,PD⊥平面ABC,AC=BC,D为AB的中点,E为AP的中点.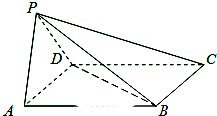 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠BAD=45°,AD=1,AB=
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠BAD=45°,AD=1,AB=