题目内容
16.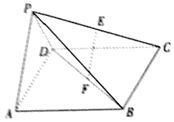 在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD、E、F,分别为PC、BD的中点.
在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD、E、F,分别为PC、BD的中点.(1)求证:EF∥平面PAD;
(2)若AB=2,求三棱锥E-DFC的体积.
分析 (1)连接AC,由正方形性质可知,AC与BD相交于点F,推导出EF∥PA,由此能证明EF∥平面PAD.
(2)由VE-DFC=VF-EDC,能求出三棱锥E-DFC的体积.
解答 证明:(1)连接AC,由正方形性质可知,AC与BD相交于点F,…(1分)
所以,在△PAC中,EF∥PA…(3分)
又PA?平面PAD,EF?平面PAD…(5分)
所以EF∥平面PAD…(6分)
解:(2)AB=2,则$PA=PD=\sqrt{2}$,
因为侧面PAD⊥底面ABCD,交线为AD,且底面是正方形,
所以CD⊥平面PAD,则CD⊥PA,
由PA2+PD2=AD2得PD⊥PA,
所以PA⊥平面PDC…(8分)
又因为EF∥PA,且$EF=\frac{1}{2}PA=\frac{{\sqrt{2}}}{2}$,
所以EF⊥平面EDC…(9分)
由CD⊥平面PAD得CD⊥PD,
所以${S_{△EDC}}=\frac{1}{2}{S_{△PDC}}=\frac{1}{2}×({\frac{1}{2}×2×\sqrt{2}})=\frac{{\sqrt{2}}}{2}$…(11分)
从而${V_{E-DFC}}={V_{F-EDC}}=\frac{1}{3}{S_{△EDC}}•EF=\frac{1}{3}×\frac{{\sqrt{2}}}{2}×\frac{{\sqrt{2}}}{2}=\frac{1}{6}$…(12分)
点评 本题考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
11.已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为30°,且|$\overrightarrow{a}$|=$\sqrt{3}$,|$\overrightarrow{b}$|=2,则$\overrightarrow{a}$•$\overrightarrow{b}$等于( )
| A. | $2\sqrt{3}$ | B. | 3 | C. | $\sqrt{6}$ | D. | $\sqrt{3}$ |
2.有下述说法:
①a>b>0是a2>b2的充要条件.
②a>b>0是$\frac{1}{a}<\frac{1}{b}$的充要条件.
③a>b>0是a3>b3的充要条件.
④a>b>0是$\sqrt{a}$>$\sqrt{b}$的充要条件.
则其中正确的说法有( )
①a>b>0是a2>b2的充要条件.
②a>b>0是$\frac{1}{a}<\frac{1}{b}$的充要条件.
③a>b>0是a3>b3的充要条件.
④a>b>0是$\sqrt{a}$>$\sqrt{b}$的充要条件.
则其中正确的说法有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
6.某程序框图如图所示,若该程序运行后输出的值是10,则a的值是( )
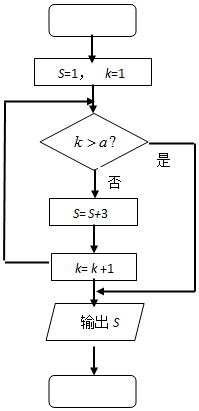

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |