题目内容
7.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左、右焦点分别是F1,F2,过F2作倾斜角为120°的直线与椭圆的一个交点为M,若MF1垂直于MF2,则椭圆的离心率为$\sqrt{3}-1$.分析 结合图形,根据Rt△MF2 F1中,在Rt△MF1F2中,F1F2=2c,∠F1F2M=60°,求出MF2,MF1,根据椭圆的定义列出关于a、c的方程,求e的值.
解答  解:如图,
解:如图,
在Rt△MF1F2中,F1F2=2c,
∵∠F1F2M=60°,
∴MF2=c,MF1=2c×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$c
MF1+MF2=c+$\sqrt{3}$c=2a,⇒e=$\frac{c}{a}$=$\sqrt{3}-1$.
故答案为$\sqrt{3}-1$.
点评 本题考查直角三角形中的边角关系,椭圆的简单性质,考查运算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.θ取一切实数时,连接A(4sinθ,6cosθ)和B(-4cosθ,6sinθ)两点的线段的中点轨迹是.( )
| A. | 圆 | B. | 椭圆 | C. | 直线 | D. | 线段 |
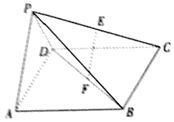 在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD、E、F,分别为PC、BD的中点.
在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD、E、F,分别为PC、BD的中点.