题目内容
9.已知数列{an}是首项为1,且公差不为0的等差数列,而等比数列{bn}的前3项分别是a1,a2,a6.(1)求数列{an}的通项公式.
(2)如果b1+b2+b3+…+bn=5,求正整数n的值.
分析 (1)设数列{an}的公差为d,由a1,a2,a6成等比数列,求出d=3,由此能求出数列{an}的通项公式.…(6分)
(2)数列{bn}的首项b1=a1=1,公比为q=$\frac{{a}_{2}}{{a}_{1}}$=4,由此能求出正整数n的值.
解答 解:(1)设数列{an}的公差为d,…(1分)
∵a1,a2,a6成等比数列,∴${{a}_{2}}^{2}={a}_{1}{a}_{6}$,…(2分)
∴(1+d)2=1×(1+5d),
由d≠0,解得d=3,…(5分)
∴an=1+(n-1)×3=3n-2.…(6分)
(2)∵等比数列{bn}的前3项分别是a1,a2,a6.
∴数列{bn}的首项b1=a1=1,公比为q=$\frac{{a}_{2}}{{a}_{1}}$=4,…(7分)
由b1+b2+b3+…+bn=5,得:
b1+b2+b3+…+bn=$\frac{1-{4}^{n}}{1-4}$=5,
解得n=2.…(11分)
∴正整数n的值是2.…(12分)
点评 本题考查等差数列的通项公式的求法,考查等比数列的前几项和为5的求法,是基础题,解题时要认真审题,注意等差数列、等比数列的性质的合理运用.

练习册系列答案
相关题目
19.2016年1月某校高三年级1600名学生参加了教育局组织的期末统考,已知数学考试成绩X~N(100,σ2)(试卷满分为150分).统计结果显示数学考试成绩在80分到120分之间的人数约为总人数的$\frac{3}{4}$,则此次统考中成绩不低于120分的学生人数约为( )
| A. | 80 | B. | 100 | C. | 120 | D. | 200 |
18.θ取一切实数时,连接A(4sinθ,6cosθ)和B(-4cosθ,6sinθ)两点的线段的中点轨迹是.( )
| A. | 圆 | B. | 椭圆 | C. | 直线 | D. | 线段 |
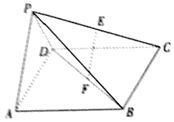 在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD、E、F,分别为PC、BD的中点.
在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD、E、F,分别为PC、BD的中点.