题目内容
6.已知p:|1-$\frac{x-1}{3}$|≤2,q:(x-1+m)(x-1-m)<0(m>0)且q是p的必要不充分条件,求实数m的取值范围.分析 分别求出关于p,q的不等式,根据q是p的必要不充分条件,得到关于m的不等式组,解出即可.
解答 解:∵|1-$\frac{x-1}{3}$|≤2,∴p:-2≤x≤10;
∵(x-1+m)(x-1-m)<0,∴q:-m+1<x<m+1,(m>0),
若q是p的必要不充分条件,
则[-2,10]⊆(-m+1,m+1),
故$\left\{\begin{array}{l}{-2>-m+1}\\{10<m+1}\end{array}\right.$,
解得:m>9.
点评 本题考查了充分必要条件,考查解不等式问题,是一道基础题.

练习册系列答案
相关题目
15.若?(p∧q)为假命题,则( )
| A. | p为真命题,q为假命题 | B. | p为假命题,q为假命题 | ||
| C. | p为真命题,q为真命题 | D. | p为假命题,q为真命题 |
 一个几何体的三视图如图所示(单位:m),正视图和俯视图的上面均是底边长为12m的等腰直角三角形,下面均是边长为6m的正方形,则该几何体的体积为216+72πm3.
一个几何体的三视图如图所示(单位:m),正视图和俯视图的上面均是底边长为12m的等腰直角三角形,下面均是边长为6m的正方形,则该几何体的体积为216+72πm3.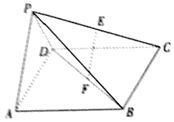 在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD、E、F,分别为PC、BD的中点.
在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD、E、F,分别为PC、BD的中点.