题目内容
设函数f(x)=
(Ⅰ)当a=3时,求函数f(x)的定义域;
(Ⅱ)若函数f(x)的定义域为R,求实数a的取值范围.
| |x-1|+|x+1|-a |
(Ⅰ)当a=3时,求函数f(x)的定义域;
(Ⅱ)若函数f(x)的定义域为R,求实数a的取值范围.
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:(Ⅰ)当a=3时,求函数f(x)的定义域;
(Ⅱ)若函数f(x)的定义域为R,求实数a的取值范围.
(Ⅱ)若函数f(x)的定义域为R,求实数a的取值范围.
解答:
解:(Ⅰ)要使函数f(x)有意义,则|x-1|+|x+1|-a≥0,
当a=3时,则|x-1|+|x+1|≥3,
解得x≥
或x≤-
,
即函数f(x)的定义域为{x|x≥
或x≤-
};
(Ⅱ)若函数f(x)的定义域为R,
则|x-1|+|x+1|-a≥0恒成立,
即|x-1|+|x+1|≥a,
∵|x-1|+|x+1|≥2,
∴a≤2,
即实数a的取值范围是(-∞,2].
当a=3时,则|x-1|+|x+1|≥3,
解得x≥
| 3 |
| 2 |
| 3 |
| 2 |
即函数f(x)的定义域为{x|x≥
| 3 |
| 2 |
| 3 |
| 2 |
(Ⅱ)若函数f(x)的定义域为R,
则|x-1|+|x+1|-a≥0恒成立,
即|x-1|+|x+1|≥a,
∵|x-1|+|x+1|≥2,
∴a≤2,
即实数a的取值范围是(-∞,2].
点评:本题主要考查函数的定义域的求解和应用,根据绝对值函数的性质是解决本题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
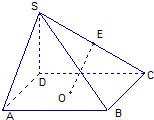 已知四棱锥S-ABCD中,底面ABCD为正方形,SD⊥DA,E为SC的中点,O为正方形ABCD的中心,AB=SD=6.
已知四棱锥S-ABCD中,底面ABCD为正方形,SD⊥DA,E为SC的中点,O为正方形ABCD的中心,AB=SD=6.