题目内容
14.已知椭圆${C_1}:\frac{x^2}{a_1^2}+\frac{y^2}{b_1^2}=1({{a_1}>{b_1}>0})$与双曲线${C_2}:\frac{x^2}{a_2^2}-\frac{y^2}{b_2^2}=1({{a_2}>0,{b_2}>0})$有相同的焦点F1,F2,点P是两曲线的一个公共点,且PF1⊥PF2,e1,e2分别是两曲线C1,C2的离心率,则$9e_1^2+e_2^2$的最小值是( )| A. | 4 | B. | 6 | C. | 8 | D. | 16 |
分析 由题意设焦距为2c,椭圆长轴长为2a1,双曲线实轴为2a2,令P在双曲线的右支上,由已知条件结合双曲线和椭圆的定义推出a12+a22=2c2,由此能求出9e12+e22的最小值.
解答 解:由题意设焦距为2c,椭圆长轴长为2a1,双曲线实轴为2a2,
令P在双曲线的右支上,
由双曲线的定义|PF1|-|PF2|=2a2,①
由椭圆定义|PF1|+|PF2|=2a1,②
又∵PF1⊥PF2,
∴|PF1|2+|PF2|2=4c2,③
①2+②2,得|PF1|2+|PF2|2=2a12+2a22,④
将④代入③,得a12+a22=2c2,
∴9e12+e22=$\frac{9{c}^{2}}{{{a}_{1}}^{2}}$+$\frac{{c}^{2}}{{{a}_{2}}^{2}}$=5+$\frac{9{{a}_{2}}^{2}}{{{2a}_{1}}^{2}}$+$\frac{{{a}_{1}}^{2}}{2{{a}_{2}}^{2}}$≥8,即$9e_1^2+e_2^2$的最小值是8.
故选:C.
点评 本题考查9e12+e22的最小值的求法,是中档题,解题时要熟练掌握双曲线、椭圆的定义,注意均值定理的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知A(-2,-1),B(2,-3),过点P(1,5)的直线l与线段AB有交点,则l的斜率的范围是( )
| A. | (-∞,-8] | B. | [2,+∞) | C. | (-∞,-8]∪[2,+∞) | D. | (-∞,-8)∪(2,+∞) |
6.若$\frac{1+2i}{a+bi}=1+i$,其中a、b为实数,则a+b的值等于( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
3.执行图中程序框图,如果输入x1=2,x2=3,x3=7,则输出的T值为( )


| A. | 0 | B. | 4 | C. | 2 | D. | 3 |
4.若函数f( x)=ax3-bx+c为奇函数,则c=( )
| A. | 0 | B. | 1 | C. | -1 | D. | -2 |
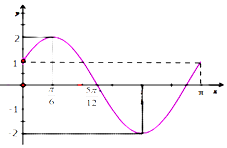 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|ϕ|<\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|ϕ|<\frac{π}{2}$)的部分图象如图所示.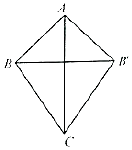 如图所示,在四边形ABCB'中,△ABC≌△AB'C,AB⊥AB',cos∠BCB'=$\frac{3}{4}$,BC=2$\sqrt{7}$,则△BCB'外接圆的面积为8π.
如图所示,在四边形ABCB'中,△ABC≌△AB'C,AB⊥AB',cos∠BCB'=$\frac{3}{4}$,BC=2$\sqrt{7}$,则△BCB'外接圆的面积为8π.