题目内容
9.设F1(-c,0),F2(c,0)是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的两个焦点,P是以F1F2为直径的圆和椭圆的一个交点,若∠PF1F2=2∠PF2F1,则椭圆的离心率等于$\sqrt{3}-1$.分析 先根据题意和圆的性质可判断出△PF1F2为直角三角形,根据∠PF1F2=2∠PF2F1,推断出∠PF1F2=60°,进而可求得PF1和PF2,再利用椭圆的定义求得a和c的关系,则椭圆的离心率可得.
解答 解:由题意△PF1F2为直角三角形,且∠P=90°,∠PF1F2=60°,F1F2=2c,
∴PF1=c,PF2=$\sqrt{3}$c,
由椭圆的定义知,PF1+PF2=c+$\sqrt{3}$c=2a,
∴离心率为e=$\frac{c}{a}$=$\frac{2}{\sqrt{3}+1}=\sqrt{3}-1$.
故答案为:$\sqrt{3}-1$.
点评 本题主要考查了椭圆的简单性质.椭圆的离心率是椭圆基本知识中重要的内容,求离心率的关键是通过挖掘题设信息求得a和c的关系,是中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
4..从编号001,002,003,…,300的300个产品中采用系统抽样的方法抽取一个样本,已知样本中编号最小的两个编号是002,017,则样本中最大的编号应该是( )
| A. | 285 | B. | 286 | C. | 287 | D. | 288 |
18.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2$\sqrt{2}$,|$\overrightarrow{a}$-$\overline{b}$|=2,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值为( )
| A. | $\frac{{\sqrt{2}}}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{{5\sqrt{2}}}{8}$ | D. | $\frac{{\sqrt{2}}}{5}$ |
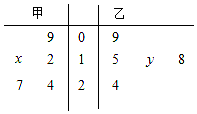 如图,茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x+y的值为( )
如图,茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x+y的值为( )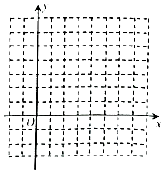 某工厂要安排生产Ⅰ、Ⅱ两种产品,这些产品要在A、B、C、D四种不同的设备上加工,按工艺规定,在一天内,产品Ⅰ每件在A、B、C、D设备上需要加工时间分别是2、2、3、0小时,产品Ⅱ每件在A、B、C、D设备上需要加工时间分别是4、1、0、3小时,A、B、C、D设备最长使用时间分别是16、8、9、9小时.设计划每天生产产品Ⅰ的数量为x(件),产品Ⅱ的数量为y(件).(x,y∈N)
某工厂要安排生产Ⅰ、Ⅱ两种产品,这些产品要在A、B、C、D四种不同的设备上加工,按工艺规定,在一天内,产品Ⅰ每件在A、B、C、D设备上需要加工时间分别是2、2、3、0小时,产品Ⅱ每件在A、B、C、D设备上需要加工时间分别是4、1、0、3小时,A、B、C、D设备最长使用时间分别是16、8、9、9小时.设计划每天生产产品Ⅰ的数量为x(件),产品Ⅱ的数量为y(件).(x,y∈N)