题目内容
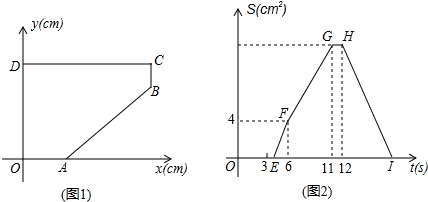
如图1,A、D分别在x轴和y轴上,CD∥x轴,BC∥y轴.点P从D点出发,以1cm/s的速度,沿五边形OABCD的边匀速运动一周.记顺次连接P、O、D三点所围成图形的面积为Scm2,点P运动的时间为ts.已知S与t之间的函数关系如图2中折线段OEFGHI所示.
(1)求A、B两点的坐标;
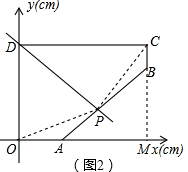
(2)若直线PD将五边形OABCD分成面积相等的两部分,求直线PD的函数关系式.
(1)求A、B两点的坐标;
(2)若直线PD将五边形OABCD分成面积相等的两部分,求直线PD的函数关系式.

考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)(1)先连接AD,设点A的坐标为(a,0),由图2得出DO=6-AO和S△AOD=4,即可得出
DO•AO=4,从而得出a的值,再根据图2得出A的坐标,再延长CB交x轴于M,根据D点的坐标得出AB=5cm,CB=1cm,即可求出AM=
=4,从而得出点B的坐标.
(2)先设点P(x,y),连PC、PO,得出S四边形DPBC的面积,再进行整理,即可得出x与y的关系,再由A,B点的坐标,求出直线AB的函数关系式,从而求出x、y的值,即可得出P点的坐标,再设直线PD的函数关系式为y=kx+4,求出K的值,即可得出直线PD的函数关系式.
| 1 |
| 2 |
| AB2-MB2 |
(2)先设点P(x,y),连PC、PO,得出S四边形DPBC的面积,再进行整理,即可得出x与y的关系,再由A,B点的坐标,求出直线AB的函数关系式,从而求出x、y的值,即可得出P点的坐标,再设直线PD的函数关系式为y=kx+4,求出K的值,即可得出直线PD的函数关系式.
解答:
解:(1)连接AD,设点A的坐标为(a,0),
由图2知,DO+OA=6cm,DO=6-AO,
由图2知S△AOD=4,
∴
DO×AO=4,
∴a2-6a+8=0,解得a=2或a=4,
由图2知,DO>3,
∴AO<3,
∴a=2,
∴A的坐标为(2,0),D点坐标为(0,4),
在图1中,延长CB交x轴于M,由图2,知AB=5cm,CB=1cm,
∴MB=3,
∴AM=
=4.
∴OM=6,
∴B点坐标为(6,3);
(2)显然点P一定在AB上.设点P(x,y),连PC.PO,
则S四边形DPBC=S△DPC+S△PBC=
S五边形OABCD=
(S矩形OMCD-S△ABM)=9,
∴
×6×(4-y)+
×1×(6-x)=9,即x+6y=12,
同理,由S四边形DPAO=9 可得2x+y=9,
由A(2,0),B(6,3)求得直线AB的函数关系式为y=
x-
,
由
解得x=
,y=
.
∴P(
,
),
设直线PD的函数关系式为y=kx+4,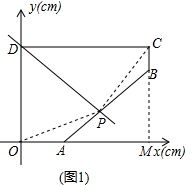
则
=
k+4,
∴k=-
,
∴直线PD的函数关系式为y=-
x+4.
由图2知,DO+OA=6cm,DO=6-AO,
由图2知S△AOD=4,
∴
| 1 |
| 2 |
∴a2-6a+8=0,解得a=2或a=4,
由图2知,DO>3,
∴AO<3,
∴a=2,
∴A的坐标为(2,0),D点坐标为(0,4),
在图1中,延长CB交x轴于M,由图2,知AB=5cm,CB=1cm,
∴MB=3,
∴AM=
| AB2-MB2 |
∴OM=6,
∴B点坐标为(6,3);
(2)显然点P一定在AB上.设点P(x,y),连PC.PO,
则S四边形DPBC=S△DPC+S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
同理,由S四边形DPAO=9 可得2x+y=9,
由A(2,0),B(6,3)求得直线AB的函数关系式为y=
| 3 |
| 4 |
| 3 |
| 2 |
由
|
解得x=
| 42 |
| 11 |
| 15 |
| 11 |
∴P(
| 42 |
| 11 |
| 15 |
| 11 |
设直线PD的函数关系式为y=kx+4,

则
| 15 |
| 11 |
| 42 |
| 11 |
∴k=-
| 29 |
| 42 |
∴直线PD的函数关系式为y=-
| 29 |
| 42 |

点评:此题考查了动点问题的函数图象,解题的关键是根据题意设出函数关系式,是难点,也是高考的重点,需熟练掌握.

练习册系列答案
相关题目
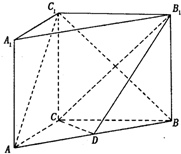 如图,AA1∥BB1∥CC1,AA1=BB1=CC1,AA1⊥面ABC且AC=3,BC=4,AB=5,AA1=4,点D为 AB的中点.
如图,AA1∥BB1∥CC1,AA1=BB1=CC1,AA1⊥面ABC且AC=3,BC=4,AB=5,AA1=4,点D为 AB的中点. 一艘轮船按照北偏西50°的方向,以15海里每小时的速度航行,一个灯塔M原来在轮船的北偏东10°方向上,经过40分钟,轮船与灯塔的距离是5
一艘轮船按照北偏西50°的方向,以15海里每小时的速度航行,一个灯塔M原来在轮船的北偏东10°方向上,经过40分钟,轮船与灯塔的距离是5