题目内容

已知集合A={x|x2-2ax+（4a-3）=0}，B={x|x2-2
2
ax+a2+a+2=0}，若A∪B=∅，试求实数a的取值范围．
考点：并集及其运算
专题：计算题,集合
分析：A∪B=∅，则A=B=∅，即二次方程x2-2ax+4a-3=0与x2-2
2
ax+a2+a+2=0均无解，利用判别式可求．
解答： 解：∵A∪B=∅，∴A=B=∅，即二次方程x2-2ax+4a-3=0与x2-2
2
ax+a2+a+2=0均无解，
∴
4a2-4(4a-3)＜0
8a2-4(a2+a+2)＜0
，∴
1＜a＜3
-1＜a＜2
，
∴1＜a＜2．
点评：本题考查并集及其运算，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
相关题目
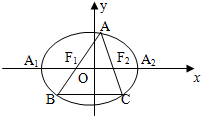如图：A1、A2是椭圆
x2
a2
+
y2
b2
=1的左右顶点，F1（-c，0），F2（c，0）是椭圆的两个焦点，若
A1F1
=λ
F1A2
，
A1F2
=μ
F2A2
，则λ+μ=
2(a2+c2)
b2
．
如果A是椭圆（a＞b＞0）上的任意一点，直线AF1、AF2分别和椭圆的交于分B、C两点，且
AF1
=λ1
F1B
，
AF2
=λ2
F2C
，那么λ1+λ2能否还为定值
2(a2+c2)
b2
？若能，请给出证明，若不能，请说明理由．
已知函数f（x）是定义在R上的奇函数，且f（x）的图象关于x=1对称，当0≤x≤1时，f（x）=x，那么f（2011.5）=
 
．
若f'（1）=
1
2
，则
lim
h→0
f(1-2k)-f(1)
3k
=
 
．
判断函数f（x）=
x+1，x＞0
x-1，x＜0
的奇偶性．
已知集合{a，
b
a
，1}也可表示为{a2，a+b，0}，则a2+b=
 
．
已知{an}的前n项和为Sn=n2+2n+1，求{an}的通项公式．
设等差数列{an}的前n项和为Sn，Sn=（
an+1
2
）2，n∈N+，求{an}的前n项和．
在△ABC中，内角A，B，C所对的边分别为a，b，c，A=120°，c＞b，a=
21
，S△ABC=
3
，求b，c．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网