题目内容
14.由曲线xy=1,直线y=x,x=3所围成的封闭图形的面积为( )| A. | $\frac{1}{2}+ln3$ | B. | 4-ln3 | C. | $\frac{9}{2}$ | D. | $\frac{11}{6}$ |
分析 确定曲线交点的坐标,确定被积区间及被积函数,利用定积分表示面积,即可得到结论.
解答 解:由曲线xy=1,直线y=x,解得x=±1.
由xy=1,x=3可得交点坐标为(3,$\frac{1}{3}$).
∴由曲线xy=1,直线y=x,x=3所围成封闭的平面图形的面积是
S=${∫}_{1}^{3}$(x-$\frac{1}{x}$)dx=($\frac{1}{2}$x2-lnx)|${\;}_{1}^{3}$=4-ln3.
故选:B.
点评 本题利用定积分计算公式,求封闭曲边图形的面积,着重考查了利用积分公式求原函数和定积分的几何意义等知识,属于基础题.

练习册系列答案
相关题目
9.K为小于9的实数时,曲线$\frac{x^2}{25}+\frac{y^2}{9}=1$与曲线$\frac{x^2}{25-K}-\frac{y^2}{K-9}=1$一定有相同的( )
| A. | 焦距 | B. | 准线 | C. | 顶点 | D. | 离心率 |
19.已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )


| A. | 2 | B. | 4 | C. | 6 | D. | 12 |
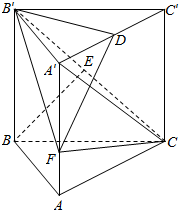 如图,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2,BB1=3,D为A1C1的中点,E为B1C的中点.
如图,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2,BB1=3,D为A1C1的中点,E为B1C的中点.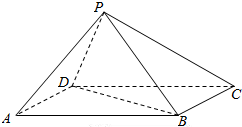 如图,四棱锥P-ABCD中,底面ABCD为矩形,AD=PD=2$\sqrt{3}$,PB=AB=6,点P在底面的正投影在DC上.
如图,四棱锥P-ABCD中,底面ABCD为矩形,AD=PD=2$\sqrt{3}$,PB=AB=6,点P在底面的正投影在DC上.