题目内容
若正数x,y满足x+3y=5xy,则x+y的最小值为 .
考点:基本不等式,基本不等式在最值问题中的应用
专题:常规题型,函数的性质及应用
分析:将x+3y=5xy转化为
+
=1,再由x+y=(
+
)•(x+y),展开后利用基本不等式可求出x+y的最小值.
| 1 |
| 5y |
| 3 |
| 5x |
| 1 |
| 5y |
| 3 |
| 5x |
解答:
解:∵正数x,y满足x+3y=5xy,∴
+
=1.
∴x+y=(x+y)•(
+
)=(
+
)+(
+
)≥2
+
=
.
当且仅当
=
,即x=
y时取等号,此时结合x+3y=5xy,
得
∴x+y≥
,可知x+y的最小值为
.
故答案为
.
| 1 |
| 5y |
| 3 |
| 5x |
∴x+y=(x+y)•(
| 1 |
| 5y |
| 3 |
| 5x |
| x |
| 5y |
| 3y |
| 5x |
| 3 |
| 5 |
| 1 |
| 5 |
|
| 4 |
| 5 |
4+2
| ||
| 5 |
当且仅当
| x |
| 5y |
| 3y |
| 5x |
| 3 |
得
|
∴x+y≥
4+2
| ||
| 5 |
4+2
| ||
| 5 |
故答案为
4+2
| ||
| 5 |
点评:本题为2012年浙江文科试题第(9)题的一个变式.容易做错,应注意等号成立的条件;“1”的替换是一个常用的技巧,应学会灵活运用.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
设F1,F2分别为双曲线
-
=1(a>0,b>0)的左、右焦点,双曲线上存在一点P使得|PF1|+|PF2|=3b,|PF1|•|PF2|=
ab,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 9 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
| D、3 |
对一个容量为N的总体抽取容量为n的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为P1,P2,P3,则( )
| A、P1=P2<P3 |
| B、P2=P3<P1 |
| C、P1=P3<P2 |
| D、P1=P2=P3 |
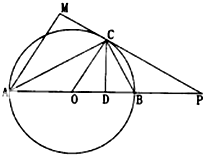 如图,已知AB是⊙O的直径,C为⊙O上一点,以C为切点的切线交AB的延长线于点P,AM⊥CP,垂足为M,CD⊥AB,垂足为D.
如图,已知AB是⊙O的直径,C为⊙O上一点,以C为切点的切线交AB的延长线于点P,AM⊥CP,垂足为M,CD⊥AB,垂足为D.