题目内容
16.已知函数f(x)=$\left\{\begin{array}{l}{x^2},x<3\\{2^x},x≥3\end{array}$,则f(f(2))=( )| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
分析 先求出f(2)=22=4,从而f(f(2))=f(4),由此能求出结果.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{x^2},x<3\\{2^x},x≥3\end{array}$,
∴f(2)=22=4,
f(f(2))=f(4)=24=16.\
故答案为:16.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
6.若函数f(x)=$\frac{1}{3}{x^3}$-x在区间(a2-26,a)上有最大值,则实数a的取值范围为( )
| A. | (-1,5) | B. | (-1,5] | C. | (-1,2) | D. | (-1,2] |
11.已知$a={2^{\frac{6}{5}}},b={({\frac{1}{8}})^{-\frac{4}{5}}},c=2{log_5}2$,则a,b,c的大小关系为( )
| A. | c<b<a | B. | c<a<b | C. | b<a<c | D. | b<c<a |
8.直线y=kx+3被圆(x-2)2+(y-3)2=4截得的弦长为$2\sqrt{3}$,则直线的斜率为( )
| A. | $\sqrt{3}$ | B. | $±\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $±\frac{{\sqrt{3}}}{3}$ |
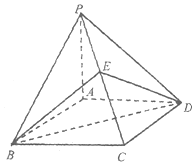 如图,已知四棱锥P-ABCD的底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,直线PB和平面ABCD所成的角为45°,E为PC的中点.
如图,已知四棱锥P-ABCD的底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,直线PB和平面ABCD所成的角为45°,E为PC的中点.