题目内容
15. 在平面直角坐标系xOy中,已知抛物线x2=2py(p>0)上的点M(m,1)到焦点F的距离为2,
在平面直角坐标系xOy中,已知抛物线x2=2py(p>0)上的点M(m,1)到焦点F的距离为2,(1)求抛物线的方程;
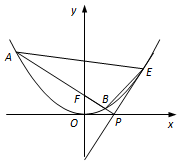
(2)如图,点E是抛物线上异于原点的点,抛物线在点E处的切线与x轴相交于点P,直线PF与抛物线相交于A,B两点,求△EAB面积的最小值.
分析 (1)求出抛物线x2=2py(p>0)的准线方程为$y=-\frac{p}{2}$,由抛物线定义,得到p=2,即可求解抛物线的方程.
(2)求出函数的$y'=\frac{1}{2}x$.设点$E(t,\;\frac{{\;{t^2}}}{4}),\;\;t≠0$,得到抛物线在点E处的切线方程为$y-\frac{{\;{t^2}}}{4}=\frac{1}{2}t(x-t)$.求出$P(\frac{t}{2},\;0)$.推出直线PF的方程,点$E(t,\;\frac{{\;{t^2}}}{4})$到直线PF的距离,联立$\left\{\begin{array}{l}y=\frac{x^2}{4}\\ 2x+ty-t=0\end{array}\right.$求出AB,表示出△EAB的面积,构造函数,通过函数的导数利用单调性求解最值即可.
解答 解:(1)抛物线x2=2py(p>0)的准线方程为$y=-\frac{p}{2}$,
因为M(m,1),由抛物线定义,知$MF=1+\frac{p}{2}$,
所以$1+\frac{p}{2}=2$,即p=2,
所以抛物线的方程为x2=4y.…3分
(2)因为$y=\frac{1}{4}{x^2}$,所以$y'=\frac{1}{2}x$.
设点$E(t,\;\frac{{\;{t^2}}}{4}),\;\;t≠0$,则抛物线在点E处的切线方程为$y-\frac{{\;{t^2}}}{4}=\frac{1}{2}t(x-t)$.
令y=0,则$x=\frac{t}{2}$,即点$P(\frac{t}{2},\;0)$.
因为$P(\frac{t}{2},\;0)$,F(0,1),所以直线PF的方程为$y=-\frac{2}{t}(x-\frac{t}{2})$,即2x+ty-t=0.
则点$E(t,\;\frac{{\;{t^2}}}{4})$到直线PF的距离为$d=\frac{{|{2t+\frac{t^3}{4}-t}|}}{{\sqrt{4+{t^2}}}}=\frac{{|t|\sqrt{4+{t^2}}}}{4}$.…5分
联立方程$\left\{\begin{array}{l}y=\frac{x^2}{4}\\ 2x+ty-t=0\end{array}\right.$消元,得t2y2-(2t2+16)y+t2=0.
因为△=(2t2+16)2-4t4=64(t2+4)>0,
所以${y_1}=\frac{{2{t^2}+16+\sqrt{64({t^2}+4)}}}{{2{t^2}}}$,${y_2}=\frac{{2{t^2}+16-\sqrt{64({t^2}+4)}}}{{2{t^2}}}$,
所以$AB={y_1}+1+{y_2}+1={y_1}+{y_2}+2=\frac{{2{t^2}+16}}{t^2}+2=\frac{{4({t^2}+4)}}{t^2}$. …7分
所以△EAB的面积为$S=\frac{1}{2}×\frac{{4({t^2}+4)}}{t^2}×\frac{{|t|\sqrt{4+{t^2}}}}{4}=\frac{1}{2}×\frac{{{{({t^2}+4)}^{\frac{3}{2}}}}}{|t|}$.
不妨设$g(x)=\frac{{{{({x^2}+4)}^{\frac{3}{2}}}}}{x}$(x>0),则$g'(x)=\frac{{{{({x^2}+4)}^{\frac{1}{2}}}}}{x^2}(2{x^2}-4)$.
因为$x∈(0,\;\sqrt{2})$时,g'(x)<0,所以g(x)在$(0,\;\sqrt{2})$上单调递减;$x∈(\sqrt{2},\;+∞)$上,g'(x)>0,所以g(x)在$(\sqrt{2},\;+∞)$上单调递增.
所以当$x=\sqrt{2}$时,$g{(x)_{min}}=\frac{{{{(2+4)}^{\frac{3}{2}}}}}{{\sqrt{2}}}=6\sqrt{3}$.
所以△EAB的面积的最小值为$3\sqrt{3}$.…10分.
点评 本题考查抛物线与直线的位置关系的应用,函数的导数与函数的最值的求法,考查转化思想以及构造法的应用,难度比较大.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{3}{2}$ | B. | $-\frac{8}{3}$ | C. | -2 | D. | 2 |
| 学生 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 甲 | 65 | 80 | 70 | 85 | 75 |
| 乙 | 80 | 70 | 75 | 80 | 70 |
| A. | 5 | B. | 4 | C. | 6 | D. | 3 |

| A. | $\frac{3}{4}<p≤\frac{7}{8}$ | B. | $p>\frac{5}{16}$ | C. | $\frac{7}{8}≤p<\frac{5}{16}$ | D. | $\frac{7}{8}<p≤\frac{5}{16}$ |