题目内容
下列命题:
(1)5>4;
(2)命题:若a>b,则a+c>b+c的否命题;
(3)“若m>0,则x2+x-m=0有实数根”的逆否命题;
(4)命题:“矩形的两条对角线相等”的逆命题.
其中假命题的个数为( )
(1)5>4;
(2)命题:若a>b,则a+c>b+c的否命题;
(3)“若m>0,则x2+x-m=0有实数根”的逆否命题;
(4)命题:“矩形的两条对角线相等”的逆命题.
其中假命题的个数为( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:(1),由于5与4的关系明确,易判断(1)正确;
(2)写出命题:“若a>b,则a+c>b+c”的否命题,再判断(2)即可;
(3)利用“原命题与其逆否命题的真假性相同”,可先判断原命题“若m>0,则x2+x-m=0有实数根”的真假性,即可判断(3);
(4)写出命题:“矩形的两条对角线相等”的逆命题,可判断(4).
(2)写出命题:“若a>b,则a+c>b+c”的否命题,再判断(2)即可;
(3)利用“原命题与其逆否命题的真假性相同”,可先判断原命题“若m>0,则x2+x-m=0有实数根”的真假性,即可判断(3);
(4)写出命题:“矩形的两条对角线相等”的逆命题,可判断(4).
解答:
解:(1)5>4,正确;
(2)命题:“若a>b,则a+c>b+c”的否命题为“若a≤b,则a+c≤b+c”,正确;
(3)“若m>0,则x2+x-m=0中△=(-1)2-4×(-m)=1+4m>1>0,故方程x2+x-m=0有实数根,为真命题,
由于原命题与其逆否命题的真假性相同,故其逆否命题为真命题,即(3)正确;
(4)命题:“矩形的两条对角线相等”的逆命题为“对角线相等的四边形是矩形”,显然错误.
综上所述,假命题的个数为1个,
故选:B.
(2)命题:“若a>b,则a+c>b+c”的否命题为“若a≤b,则a+c≤b+c”,正确;
(3)“若m>0,则x2+x-m=0中△=(-1)2-4×(-m)=1+4m>1>0,故方程x2+x-m=0有实数根,为真命题,
由于原命题与其逆否命题的真假性相同,故其逆否命题为真命题,即(3)正确;
(4)命题:“矩形的两条对角线相等”的逆命题为“对角线相等的四边形是矩形”,显然错误.
综上所述,假命题的个数为1个,
故选:B.
点评:本题考查命题的真假判断与应用,着重考查四种命题之间的关系及真假判断,是基本知识的考查.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
已知全集U=R,集合A={y|y=-2x,x∈R},B={y|y=x2-3x,x∈R},则A∩∁UB=( )
A、{x|=
| ||
B、{x|x<-
| ||
| C、{(1,-2)} | ||
D、{x|x≤-
|
已知函数f(x)的定义域为R,且对任意x∈R都有f(x)=f(x-1)+f(x+1),若f(-1)=2,f(1)=3则f(2012)+f(-2012)=( )
| A、-5 | B、-10 |
| C、5055 | D、5060 |
设等差数列{an}的前n项和为Sn,已知a1=-11,a3+a7=-6,当Sn取得最小值是,n=( )
| A、5 | B、6 | C、7 | D、8 |
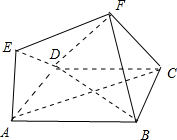 如图所示,已知在多面体ABCDEF中,底面是正方形,EA⊥平面ABCD,EF∥AC且AC=2EF,AB=2AE=2
如图所示,已知在多面体ABCDEF中,底面是正方形,EA⊥平面ABCD,EF∥AC且AC=2EF,AB=2AE=2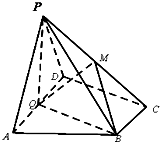 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=