题目内容
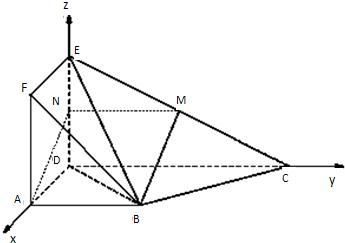
 如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=
如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=| 1 |
| 2 |
(1)当点M是EC中点时,求证:BM∥平面ADEF;
(2)当EM=2MC时,求平面BDM与平面ABF所成锐二面角的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)取DE中点N,连接MN,AN,由三角形中位线定理,结合已知中AB∥CD,AB=AD=2,CD=4,易得四边形ABMN为平行四边形,所以BM∥AN,再由线面平面的判定定理,可得BM∥平面ADEF;
(2)建立空间直角坐标系,用坐标表示点与向量,利用EM=2MC,求出平面BDM的法向量、平面ABF的法向量,利用向量的夹角公式,即可求平面BDM与平面ABF所成锐二面角的余弦值.
(2)建立空间直角坐标系,用坐标表示点与向量,利用EM=2MC,求出平面BDM的法向量、平面ABF的法向量,利用向量的夹角公式,即可求平面BDM与平面ABF所成锐二面角的余弦值.
解答:
证明:(1)取DE中点N,连接MN,AN
在△EDC中,M、N分别为EC,ED的中点,所以MN∥CD,且MN=
CD.
由已知AB∥CD,AB=
CD,
所以MN∥AB,且MN=AB.
所以四边形ABMN为平行四边形,所以BM∥AN
又因为AN?平面ADEF,且BM?平面ADEF,
所以BM∥平面ADEF;
解:(Ⅱ)以直线DA、DC、DE分别为x轴、y轴、z轴建立空间直角坐标系,
∵AB=AD=
CD=2,
则A(2,0,0),B(2,2,0),C(0,4,0),E(0,0,2),
则∵EM=2MC,
∴
=
=(0,-
,
),
又∵
=(2,2,0),
=
+
=(0,
,
),
设平面BDM的法向量
=(x,y,z),
则
,
即
,
∴令y=-1,取
=(1,-1,4),
∵平面ABF的法向量
=(1,0,0),
∴cos<
,
>=
=
,
∴平面BDM与平面ABF所成锐二面角的余弦值为
.
在△EDC中,M、N分别为EC,ED的中点,所以MN∥CD,且MN=
| 1 |
| 2 |
由已知AB∥CD,AB=
| 1 |
| 2 |
所以MN∥AB,且MN=AB.
所以四边形ABMN为平行四边形,所以BM∥AN
又因为AN?平面ADEF,且BM?平面ADEF,
所以BM∥平面ADEF;
解:(Ⅱ)以直线DA、DC、DE分别为x轴、y轴、z轴建立空间直角坐标系,
∵AB=AD=
| 1 |
| 2 |
则A(2,0,0),B(2,2,0),C(0,4,0),E(0,0,2),

则∵EM=2MC,
∴
| CM |
| 1 |
| 3 |
| CE |
| 4 |
| 3 |
| 2 |
| 3 |
又∵
| DB |
| DM |
| DC |
| CM |
| 8 |
| 3 |
| 2 |
| 3 |
设平面BDM的法向量
| n1 |
则
|
即
|
∴令y=-1,取
| n1 |
∵平面ABF的法向量
| n2 |
∴cos<
| n1 |
| n2 |
| 1 | ||
1•
|
| ||
| 6 |
∴平面BDM与平面ABF所成锐二面角的余弦值为
| ||
| 6 |
点评:本题考查的知识点是二面角的平面角及求法,直线与平面平行的判定,熟练掌握利用向量知识解决立体几何问题是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
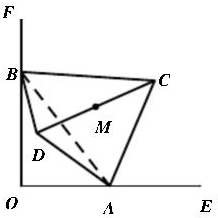 如图,一个棱长为2的正四面体ABCD的两个顶点A,B分别在一个直角(∠EOF)的两边OE,OF上运动,M是棱CD的中点,设点M与O点的距离为d,则d的取值范围是
如图,一个棱长为2的正四面体ABCD的两个顶点A,B分别在一个直角(∠EOF)的两边OE,OF上运动,M是棱CD的中点,设点M与O点的距离为d,则d的取值范围是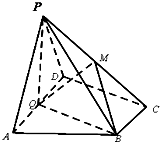 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=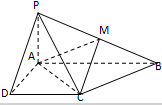 如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC= 已知B(-1,1)是椭圆
已知B(-1,1)是椭圆