题目内容
如图树顶A离地面am,树上另一点B离地面bm.在离地面cm的C处看此树,离此树多远时看A、B的视角最大?
考点:解三角形的实际应用
专题:计算题,解三角形,不等式的解法及应用
分析:过点C作CD⊥AB,设CD=x,根据已知中树顶A距地面a米,树上另一点B距地面b米,人眼C离地面c米.我们易求出tan∠ACB,即tan(∠ACD-∠BCD)的表达式,进而根据基本不等式,求出tan∠ACB的范围及tan∠ACB取最大值时x的值,进而得到答案.
解答:
解:如图,过点C作CD⊥AB,则AD=a-c,BD=b-c,设CD=x.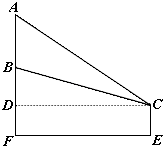
由图可知:tan∠ACB=tan(∠ACD-∠BCD)=
=
=
≤
,
当且仅当x=
,
即有x=
时,等号成立即有取得最大值.
则离此树
m时,看A、B的视角最大.

由图可知:tan∠ACB=tan(∠ACD-∠BCD)=
| tan∠ACD-tan∠BCD |
| 1+tan∠ACD•tan∠BCD |
=
| ||||
1+
|
| a-b | ||
x+
|
| a-b | ||
2
|
当且仅当x=
| (a-c)(b-c) |
| x |
即有x=
| (a-c)(b-c) |
则离此树
| (a-c)(b-c) |
点评:本题考查的知识点是三角函数的实际应用,两角差的正切公式,及基本不等式,其中构造适当的三角形,将问题转化为一个三角函数问题是解答本题的关键.

练习册系列答案
相关题目
设等差数列{an}的前n项和为Sn,已知a1=-11,a3+a7=-6,当Sn取得最小值是,n=( )
| A、5 | B、6 | C、7 | D、8 |
已知F1,F2分别为双曲线
-
=1(a>0,b>0)的左右焦点,如果双曲线上存在一点P,使得F2关于直线PF1的对称点恰在y轴上,则该双曲线的离心率e的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、e>
| ||||
B、1<e<
| ||||
C、e>
| ||||
D、1<e<
|
 如图,在一个边长为2的正方形中随机撒入200粒的豆子,恰有120粒落在阴影区域里,则该阴影部分的面积约为( )
如图,在一个边长为2的正方形中随机撒入200粒的豆子,恰有120粒落在阴影区域里,则该阴影部分的面积约为( )A、
| ||
B、
| ||
C、
| ||
D、
|
绝对值等于其相反数的数一定是( )
| A、负数 | B、正数 |
| C、负数或零 | D、正数或零 |
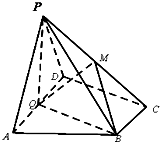 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=