题目内容
已知O是坐标原点,A,B是直线l:x-y+t=0与圆C:x2+y2=4的两个不同交点,若|
|≤|
+
|,则实数t的取值范围是( )
| AB |
| OA |
| OB |
A、(-2
| ||||
B、[2,2
| ||||
C、(-2
| ||||
D、[-2
|
考点:直线和圆的方程的应用
专题:计算题,平面向量及应用,直线与圆
分析:将已知向量式两边平方,得到∠AOB≤90°,再直线和圆相切,及直线和圆相交所得圆心角为直角的情况,再结合条件即可得到所求范围.
解答:
解:由于
=
-
,
则|
-
|≤|
+
|,
两边同时平方整理得
•
≥0,
则∠AOB≤90°,又直线l:x-y+t=0的斜率为1,
经过(-2,0),(0,2)或(0,-2),(2,0)时恰好满足∠AOB=90°,
此时t=2或-2;
当l:x-y+t=0与圆相切时是一种临界状态,此时d=
=2,
解得,t=2
或t=-2
,
由于直线l:x-y+t=0与圆C:x2+y2=4的两个不同交点,
则t∈(-2
,-2]∪[2,2
).
故选C.
| AB |
| OB |
| OA |
则|
| OB |
| OA |
| OA |
| OB |
两边同时平方整理得
| OA |
| OB |
则∠AOB≤90°,又直线l:x-y+t=0的斜率为1,
经过(-2,0),(0,2)或(0,-2),(2,0)时恰好满足∠AOB=90°,
此时t=2或-2;
当l:x-y+t=0与圆相切时是一种临界状态,此时d=
| |t| | ||
|
解得,t=2
| 2 |
| 2 |
由于直线l:x-y+t=0与圆C:x2+y2=4的两个不同交点,
则t∈(-2
| 2 |
| 2 |
故选C.
点评:本题考查平面向量的数量积的性质,考查直线和圆的位置关系,考查运算能力,属于中档题.

练习册系列答案
相关题目
已知全集U=R,集合A={y|y=-2x,x∈R},B={y|y=x2-3x,x∈R},则A∩∁UB=( )
A、{x|=
| ||
B、{x|x<-
| ||
| C、{(1,-2)} | ||
D、{x|x≤-
|
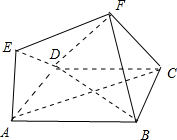 如图所示,已知在多面体ABCDEF中,底面是正方形,EA⊥平面ABCD,EF∥AC且AC=2EF,AB=2AE=2
如图所示,已知在多面体ABCDEF中,底面是正方形,EA⊥平面ABCD,EF∥AC且AC=2EF,AB=2AE=2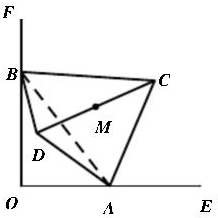 如图,一个棱长为2的正四面体ABCD的两个顶点A,B分别在一个直角(∠EOF)的两边OE,OF上运动,M是棱CD的中点,设点M与O点的距离为d,则d的取值范围是
如图,一个棱长为2的正四面体ABCD的两个顶点A,B分别在一个直角(∠EOF)的两边OE,OF上运动,M是棱CD的中点,设点M与O点的距离为d,则d的取值范围是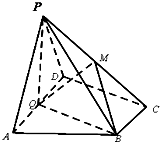 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=