题目内容
19.椭圆E的焦点在x轴上,中心在原点,其短轴上的两个顶点和两个焦点恰为边长是2的正方形的顶点,则椭圆E的标准方程为( )| A. | $\frac{x^2}{2}+\frac{y^2}{{\sqrt{2}}}=1$ | B. | $\frac{x^2}{2}+{y^2}=1$ | C. | $\frac{x^2}{4}+\frac{y^2}{2}=1$ | D. | $\frac{y^2}{4}+\frac{x^2}{2}=1$ |
分析 用正方形的正方形边长为2,得|AF1|=|AF2|=a=2,|F1F2|=2$\sqrt{2}$,c=b即可
解答 解:设左右焦点为F1、F2,上顶点为A,正方形边长=2,
∴|AF1|=|AF2|=a=2,|F1F2|=2$\sqrt{2}$,c=b=$\sqrt{2}$,
则椭圆E的标准方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$.
故选:C.
点评 本题考查用待定系数法求椭圆的标准方程,属于基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
10.“a=3”是“直线ax-2y-1=0与直线6x-4y+1=0平行”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
7.已知函数f(x)=Asin(2x+φ)-$\frac{1}{2}$(A>0,0<φ<$\frac{π}{2}$)的图象在y轴上的截距为1,且关于直线x=$\frac{π}{12}$对称,若对于任意的x∈[0,$\frac{π}{2}$],都有m2-3m≤f(x),则实数m的取值范围为( )
| A. | [1,$\frac{3}{2}$] | B. | [1,2] | C. | [$\frac{3}{2}$,2] | D. | [$\frac{3-\sqrt{3}}{2}$,$\frac{3+\sqrt{3}}{2}$] |
11.在Rt△ABC中,∠B=60°过直角顶点A在∠BAC内随机作射线AD,交斜边BC于点D,则BD>BA的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
8.在复平面内,复数$z=\frac{-1+i}{2-i}$(i为虚数单位)的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
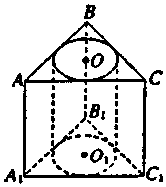 如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,其高为6cm,底面三角形的边长分别为3cm,4cm,5cm,以上、下底面的内切圆为底面,挖去一个圆柱,求剩余部分几何体的体积V.
如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,其高为6cm,底面三角形的边长分别为3cm,4cm,5cm,以上、下底面的内切圆为底面,挖去一个圆柱,求剩余部分几何体的体积V.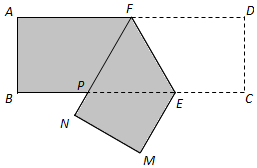 如图,某机械厂要将长6m,宽2m的长方形铁皮ABCD进行裁剪.已知点F为AD的中点,点E在边BC上,裁剪时先将四边形CDFE沿直线EF翻折到MNFE处(点C,D分别落在直线BC下方点M,N处,FN交边BC于点P),再沿直线PE裁剪.
如图,某机械厂要将长6m,宽2m的长方形铁皮ABCD进行裁剪.已知点F为AD的中点,点E在边BC上,裁剪时先将四边形CDFE沿直线EF翻折到MNFE处(点C,D分别落在直线BC下方点M,N处,FN交边BC于点P),再沿直线PE裁剪.