题目内容
5.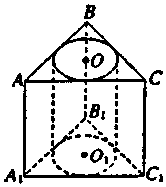 如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,其高为6cm,底面三角形的边长分别为3cm,4cm,5cm,以上、下底面的内切圆为底面,挖去一个圆柱,求剩余部分几何体的体积V.
如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,其高为6cm,底面三角形的边长分别为3cm,4cm,5cm,以上、下底面的内切圆为底面,挖去一个圆柱,求剩余部分几何体的体积V.
分析 求出三棱柱ABC-A1B1C1的体积和圆柱的体积,由$V={V_{三棱柱ABC-{A_1}{B_1}{C_1}}}-{V_{圆柱O{O_1}}}$,能求出剩余部分几何体的体积V.
解答 解:∵三棱柱ABC-A1B1C1的侧棱垂直于底面,其高为6cm,
底面三角形的边长分别为3cm,4cm,5cm,
∴△ABC是直角边长为3cm,4cm的直角三角形,
∴${V_{三棱柱ABC-{A_1}{B_1}{C_1}}}=\frac{3×4}{2}×6=36(c{m^3})$.
…(3分)
设圆柱底面圆的半径为r,
则$r=\frac{{2{S_{△ABC}}}}{AB+BC+AC}=\frac{2×3×4}{3+4+5}=1$,…(6分)
${V_{圆柱O{O_1}}}=π{r^2}h=6π(c{m^3})$. …(9分)
所以$V={V_{三棱柱ABC-{A_1}{B_1}{C_1}}}-{V_{圆柱O{O_1}}}=(36-6π)c{m^3}$.
…(10分)
点评 本题考查剩余部分几何体的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
13.设l,m,n表示三条直线,α,β,γ表示三个平面,则下面命题中不成立的是( )
| A. | 若l⊥α.m⊥α,则l∥m | |
| B. | 若m?β,m⊥l,n是l在β内的射影,则m⊥n | |
| C. | 若m?α,n?α,m∥n,则n∥α | |
| D. | 若α⊥γ,β⊥γ,则α∥β. |
20.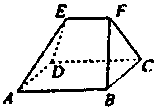 如图,在多面体ABCDEF中,四边形ABCD是边长为3的正方形,EF∥AB,EF=$\frac{3}{2}$,且点E到平面ABCD的距离为2,则该多面体的体积为( )
如图,在多面体ABCDEF中,四边形ABCD是边长为3的正方形,EF∥AB,EF=$\frac{3}{2}$,且点E到平面ABCD的距离为2,则该多面体的体积为( )
 如图,在多面体ABCDEF中,四边形ABCD是边长为3的正方形,EF∥AB,EF=$\frac{3}{2}$,且点E到平面ABCD的距离为2,则该多面体的体积为( )
如图,在多面体ABCDEF中,四边形ABCD是边长为3的正方形,EF∥AB,EF=$\frac{3}{2}$,且点E到平面ABCD的距离为2,则该多面体的体积为( )| A. | $\frac{9}{2}$ | B. | 5 | C. | 6 | D. | $\frac{15}{2}$ |
10.书架上有2本不同的语文书,1本数学书,从中任意取出2本,取出的书恰好都是语文书的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
19.椭圆E的焦点在x轴上,中心在原点,其短轴上的两个顶点和两个焦点恰为边长是2的正方形的顶点,则椭圆E的标准方程为( )
| A. | $\frac{x^2}{2}+\frac{y^2}{{\sqrt{2}}}=1$ | B. | $\frac{x^2}{2}+{y^2}=1$ | C. | $\frac{x^2}{4}+\frac{y^2}{2}=1$ | D. | $\frac{y^2}{4}+\frac{x^2}{2}=1$ |
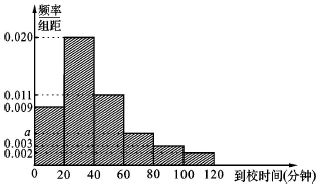 某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图:
某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图: