题目内容
11.数列{an}是公差为d(d≠0)的等差数列,Sn为其前n项和,a1,a2,a5成等比数列,(Ⅰ)证明S1,S3,S9成等比数列;
(Ⅱ)设a1=1,bn=a${\;}_{{2}^{n}}$,求数列{bn}的前n项和Tn.
分析 (Ⅰ)运用等差数列的通项公式和等比数列中项的性质,解方程可得d=2a1,再由等差数列的求和公式,结合等比数列中项性质,即可得证;
(Ⅱ)求出bn=a${\;}_{{2}^{n}}$,=a1+(2n-1)d=1+2(2n-1)=2n+1-1,再由分组求和,结合等比数列的求和公式,计算即可得到所求和.
解答 (Ⅰ)证明:数列{an}是公差为d(d≠0)的等差数列,
Sn为其前n项和,a1,a2,a5成等比数列,
可得a22=a1a5,
即为(a1+d)2=a1(a1+4d),
化简可得d=2a1,
S1S9=a1(9a1+36d)=81a12,S3=3a1+3d=9a1,
可得S1S9=S32,
即为S1,S3,S9成等比数列;
(Ⅱ)解:设a1=1,bn=a${\;}_{{2}^{n}}$,=a1+(2n-1)d=1+2(2n-1)=2n+1-1,
数列{bn}的前n项和Tn=(4+8+…+2n+1)-n
=$\frac{4(1-{2}^{n})}{1-2}$-n=2n+2-4-n.
点评 本题考查等差数列的通项公式和求和公式的运用,等比数列中项的性质,考查数列的求和方法:分组求和,注意运用等比数列的求和公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
1.若同时掷两枚骰子,则向上的点数和是6的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{5}{36}$ | D. | $\frac{5}{18}$ |
6.设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,其焦距为2c,点Q(c,$\frac{a}{2}$)在椭圆的内部,点P是椭圆C上的动点,且|PF1|+|PQ|<5|F1F2|恒成立,则椭圆离心率的取值范围是( )
| A. | ($\frac{1}{5}$,$\frac{\sqrt{2}}{2}$) | B. | ($\frac{1}{4}$,$\frac{\sqrt{2}}{2}$) | C. | ($\frac{1}{3}$,$\frac{\sqrt{2}}{2}$) | D. | ($\frac{2}{5}$,$\frac{\sqrt{2}}{2}$) |
16.过直线y=x+1上的点P作圆C:(x-1)2+(y-6)2=2的两条切线l1,l2,当直线l1,l2关于直线y=x+1对称时,|PC|=( )
| A. | 3 | B. | 2$\sqrt{2}$ | C. | 1+$\sqrt{2}$ | D. | 2 |
2.如图是由圆柱与两个半球组合而成的几何体的三视图,则该几何体的体积与表面积分别为( )
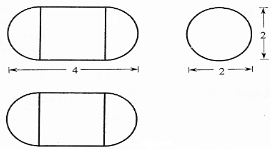

| A. | $\frac{10}{3}π,8π$ | B. | $\frac{16}{3}π,8π$ | C. | $\frac{10}{3}π,10π$ | D. | $\frac{16}{3}π,10π$ |
 如图所示,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从B点开始由左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x(0≤x≤7),左边部分的面积为y,求y与x之间的函数关系式,画出程序框图,并写出程序.
如图所示,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从B点开始由左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x(0≤x≤7),左边部分的面积为y,求y与x之间的函数关系式,画出程序框图,并写出程序.