如图是由圆柱与两个半球组合而成的几何体的三视图.则该几何体的体积与表面积分别为( )A．$\frac{10}{3}π.8π$B．$\frac{16}{3}π.8π$C．$\frac{10}{3}π.10π$D．$\frac{16}{3}π.10π$ 题目和参考答案——青夏教育精英家教网——

题目内容

2．如图是由圆柱与两个半球组合而成的几何体的三视图，则该几何体的体积与表面积分别为（　　）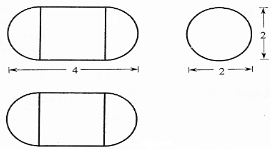

A．

$\frac{10}{3}π，8π$

B．

$\frac{16}{3}π，8π$

C．

$\frac{10}{3}π，10π$

D．

$\frac{16}{3}π，10π$

分析利用圆柱与球的体积、表面积计算公式即可得出．

解答解：该几何体的体积V=π×1²×2+$\frac{4}{3}π×{1}^{3}$=$\frac{10π}{3}$．
表面积S=2π×1×2+4π×1²=8π．
故选：A．

点评本题考查了圆柱与球的三视图及其体积、表面积计算公式，考查了推理能力与计算能力，属于基础题．

练习册系列答案

初中同步实验检测卷系列答案

各地期末真题汇编精选卷系列答案

全优中考全国中考试题精选精析系列答案

自主学英语系列答案

阅读授之以渔系列答案

浙江省普通高中作业本系列答案

实验班中考总复习系列答案

亮点激活期末冲刺大试卷系列答案

全优学习达标训练系列答案

毕业会考阶梯模拟卷系列答案

相关题目

11．数列{a_n}是公差为d（d≠0）的等差数列，S_n为其前n项和，a₁，a₂，a₅成等比数列，
（Ⅰ）证明S₁，S₃，S₉成等比数列；
（Ⅱ）设a₁=1，b_n=a${\;}_{{2}^{n}}$，求数列{b_n}的前n项和T_n．

13．设$\overrightarrow{a}$、$\overrightarrow{b}$分别是两条异面直线l₁、l₂的方向向量，向量$\overrightarrow{a}$、$\overrightarrow{b}$的夹角的取值范围为A．l₁、l₂所成的角的取值范围为B，则“a∈A”是“a∈B”的（　　）

	A．	充要条件		B．	充分不必要条件
	C．	必要不充分条件		D．	既不充分也不必要条件

10．已知定义在R上的函数f（x）=e^-|x|，记a=f（log_0.53），b=f（log₂5），c=f（0），则a，b，c的大小关系为（　　）

17．已知Rt△ABC中，$∠A=\frac{π}{2}$，以B，C为焦点的双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）经过点A，且与AB边交于点D，若|AD|=2|BD|，则该双曲线的离心率为（　　）

$\frac{{\sqrt{10}}}{2}$

$\frac{{\sqrt{5}}}{2}$

7．中国宋代的数学家秦九韶曾提出“三斜求积术”，即假设在平面内有一个三角形，边长分别为a，b，c，三角形的面积S可由公式$S=\sqrt{p（p-a）（p-b）（p-c）}$求得，其中p为三角形周长的一半，这个公式也被称为海伦-秦九韶公式，现有一个三角形的边长满足a+b=12，c=8，则此三角形面积的最大值为（　　）

14．设函数f（x）=x²e^-x，g（x）=xlnx．
（1）若F（x）=f（x）-g（x），证明：F（x）在（0，+∞）上存在唯一零点；
（2）设函数h（x）=min{f（x），g（x）}，（min{a，b}表示a，b中的较小值），若h（x）≤λ，求λ的取值范围．

11．已知抛物线C：y²=2px（p＞0）的焦点为F，直线y=4与C的交点为P，与y轴的交点为Q，且|PF|=$\frac{3}{2}$|PQ|，则抛物线C的方程为y²=4$\sqrt{2}$x，点P的坐标为（2$\sqrt{2}$，4）．

12．已知A是双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a，b＞0）的右顶点，过左焦点F与y轴平行的直线交双曲线于P，Q两点，若△APQ是锐角三角形，则双曲线C的离心率范围是（　　）

$（{1，\sqrt{2}}）$

$（{1，\sqrt{3}}）$