题目内容
已知函数f(x)=lnx-ax在区间[1,3]上有两个不同的零点,则实数a的取值范围是 .
考点:根的存在性及根的个数判断
专题:计算题,作图题,函数的性质及应用
分析:函数f(x)=lnx-ax在区间[1,3]上有两个不同的零点可化为y=lnx与y=ax在[1,3]上有两个不同的交点,作图求解.
解答:
解:函数f(x)=lnx-ax在区间[1,3]上有两个不同的零点可化为
y=lnx与y=ax在[1,3]上有两个不同的交点,
作函数y=lnx与y=ax在[1,3]上的图象如下,

当直线与y=lnx相切时,
则
=
,
解得,x=e;
故直线与y=lnx相切时,切线的斜率a=
;
当过点(3,ln3)时,a=
;
故实数a的取值范围是[
,
);
故答案为:[
,
).
y=lnx与y=ax在[1,3]上有两个不同的交点,
作函数y=lnx与y=ax在[1,3]上的图象如下,

当直线与y=lnx相切时,
则
| lnx |
| x |
| 1 |
| x |
解得,x=e;
故直线与y=lnx相切时,切线的斜率a=
| 1 |
| e |
当过点(3,ln3)时,a=
| ln3 |
| 3 |
故实数a的取值范围是[
| ln3 |
| 3 |
| 1 |
| e |
故答案为:[
| ln3 |
| 3 |
| 1 |
| e |
点评:本题考查了数形结合的应用及函数的零点与函数的图象的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=
是( )
| 1 | ||
|
| A、(3,+∞)上的增函数 |
| B、[3,+∞)上的增函数 |
| C、(3,+∞)上的减函数 |
| D、[3,+∞)上的增函数 |
已知直线l,直线b,平面α,下列说法正确的是( )
| A、若l∥b,b?α,那么l平行α内的无数条直线 |
| B、若l?α,则l∥α |
| C、若l⊥b,b?α,则l⊥α |
| D、l平行于α内的无数直线,则l∥α |
函数y=sin2x的图象的一条对称轴的方程是( )
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
D、x=
|
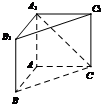 如图,直三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC.若AB=AC=AA1=1,BC=
如图,直三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC.若AB=AC=AA1=1,BC=| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
 已知数列{an}的各项均为正数,观察如图程序框图,当k=2时,有S=8,当k=3时,有S=15.
已知数列{an}的各项均为正数,观察如图程序框图,当k=2时,有S=8,当k=3时,有S=15.