题目内容
函数y=
是（ ）
| 1 | ||
|
| A、（3，+∞）上的增函数 |
| B、[3，+∞）上的增函数 |
| C、（3，+∞）上的减函数 |
| D、[3，+∞）上的增函数 |
考点：函数单调性的判断与证明,函数的定义域及其求法
专题：导数的综合应用
分析：对函数求导，根据导数符号即可判断出该函数在其定义域上的单调性．
解答：
解：y′=-
＜0；
∴函数y=
是（3，+∞）上的减函数．
故选C．
| 1 | ||
2
|
∴函数y=
| 1 | ||
|
故选C．
点评：考查根据导数符号判断函数单调性的方法，注意要正确求导．
练习册系列答案
快捷英语周周练系列答案
相关题目
若等边△ABC的边长为2，平面内一点O满足
=
+
，则
•
等于（ ）
| CO |
| 1 |
| 2 |
| CB |
| 1 |
| 3 |
| CA |
| OA |
| OB |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
密码锁上的密码是一种四位数字号码，每位上的数字可在0到9这10个数字中选取，某人忘记密码的最后一位数字，如果随意按下密码的最后一位数字，则正好按对密码的概率（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
用1，2，3，4，5这5个数字可以组成没有重复数字的二位数的个数为（ ）
| A、25 |
| B、20 |
| C、10 |
| D、52 |
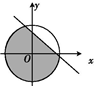区域D是平面直角坐标系中由到原点距离不大于1的点组成，在区域D内任取一点（x，y），该点满足x+y＜
| ||
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|