题目内容
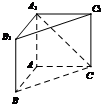如图，直三棱柱ABC-A1B1C1中，侧棱AA1⊥平面ABC．若AB=AC=AA1=1，BC=| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
考点：异面直线及其所成的角
专题：空间角
分析：求出三角形的三个边长，然后求解异面直线所成角即可．
解答：
解：因为几何体是棱柱，BC∥B1C1，则直线A1C与BC所成的角为就是异面直线A1C与B1C1所成的角．
直三棱柱ABC-A1B1C1中，侧棱AA1⊥平面ABC．若AB=AC=AA1=1，BC=
，BA1=
=
，CA1=
=
，
三角形BCA1是正三角形，异面直线所成角为60°．
故选：C．
直三棱柱ABC-A1B1C1中，侧棱AA1⊥平面ABC．若AB=AC=AA1=1，BC=
| 2 |
| AA12+AB2 |
| 2 |
| AA12+AC2 |
| 2 |
三角形BCA1是正三角形，异面直线所成角为60°．
故选：C．
点评：本题考查异面直线所成角的求法，考查计算能力．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
函数y=cos（2x+
）的图象的一条对称轴方程是（ ）
| π |
| 2 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
| D、x=π |
已知集合A={（x，y）|
}，B={（x，y）|ax-2y-2≤0}，若A⊆B，则实数a的取值范围是（ ）
|
| A、[-1，2] |
| B、[-2，2] |
| C、（-1，2] |
| D、（-2，2） |
已知f（x）=
，若f（x）=3，则x的值为（ ）
|
|
A、1或
| ||||
B、±
| ||||
C、
| ||||
D、1或±
|
设a=log
π，b=（
）-0.8，c=lgπ，则（ ）
| 1 |
| 2013 |
| 1 |
| 5 |
| A、a＜b＜c |
| B、a＜c＜b |
| C、c＜a＜b |
| D、b＜a＜c |