题目内容
已知直线l，直线b，平面α，下列说法正确的是（ ）
| A、若l∥b，b?α，那么l平行α内的无数条直线 |
| B、若l?α，则l∥α |
| C、若l⊥b，b?α，则l⊥α |
| D、l平行于α内的无数直线，则l∥α |
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：根据线面关系以及线面平行、线面垂直的判定定理解答．
解答：
解：对于A，若l∥b，b?α，根据线面平行的判定定理可以得到l平行于平面内所有与直线b平行的直线，有无数条；故A正确；
对于B，l?α，包括直线l与α平行或者相交；故B错误；
对于C，l⊥b，b?α，l与α可能平行或者一般相交；故C错误；
对于D，l平行于α内的无数直线，直线l与α可能平行或者在α内；故D错误；
故选：A．
对于B，l?α，包括直线l与α平行或者相交；故B错误；
对于C，l⊥b，b?α，l与α可能平行或者一般相交；故C错误；
对于D，l平行于α内的无数直线，直线l与α可能平行或者在α内；故D错误；
故选：A．
点评：本题考查了线面平行的判定定理以及线面垂直的判定定理的运用梦舒雅掌握定理是关键．
练习册系列答案
相关题目
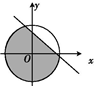区域D是平面直角坐标系中由到原点距离不大于1的点组成，在区域D内任取一点（x，y），该点满足x+y＜
| ||
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知m、n是两条不同的直线，α、β是两个不同的平面，则下列命题中正确的是（ ）
| A、若m⊥α，n⊥β，且m⊥n，则α⊥β |
| B、若m∥α，n∥β，且m∥n，则α∥β |
| C、若m⊥α，n∥β，且m⊥n，则α⊥β |
| D、若m⊥α，n∥β，且m∥n，则α∥β |
设f（x）是定义在（0，+∞）上的增函数，当a，b∈（0，+∞）时，均有f（a•b）=f（a）+f（b），已知f（2）=1．求：
（1）f（1）和f（4）的值；
（2）不等式f（x2）＜2f（4）的解集．
（1）f（1）和f（4）的值；
（2）不等式f（x2）＜2f（4）的解集．
函数y=|x-1|的图象的对称轴方程为（ ）
| A、x=1 | B、x=-1 |
| C、y=1 | D、y=-1 |
函数y=cos（2x+
）的图象的一条对称轴方程是（ ）
| π |
| 2 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
| D、x=π |