题目内容
下列函数是增函数的是( )
A、y=tanx(x∈(0,
| ||||
B、y=x
| ||||
| C、y=cosx(x∈(0,π)) | ||||
| D、y=2-x |
考点:正切函数的单调性
专题:函数的性质及应用,三角函数的图像与性质
分析:根据函数的定义域直接确定函数的单调性
解答:
解:(1)y=tanx(x∈(0,
)∪(
,π))函数在定义域x∈(0,
)∪(
,π)不具有单调性.
(2)y=cosx(x∈(0,π))在定义域内为单调递减函数.
(3)y=2-x在定义域内为单调递减函数.
故选B
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
(2)y=cosx(x∈(0,π))在定义域内为单调递减函数.
(3)y=2-x在定义域内为单调递减函数.
故选B
点评:本题考查的知识要点:函数的单调性与定义域的关系

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
定义在R上的函数f(x)满足xf′(x)≤0,且y=f(x)为偶函数,当|x1|<|x2|时,有( )
| A、f(x1)>f(x2) |
| B、f(x1)=f(x2) |
| C、f(x1)<f(x2) |
| D、f(|x2|)>f(x1) |
已知等差数列{an}的前n项和为Sn(n∈N+),且an=2n+λ,若数列{Sn}在n≥7时为递增数列,则实数λ的取值范围为( )
| A、(-15,+∞) |
| B、[-15,+∞) |
| C、[-16,+∞) |
| D、(-16,+∞) |
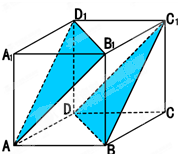 已知正方体ABCD-A1B1C1D1.求证:
已知正方体ABCD-A1B1C1D1.求证: