题目内容
5.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了4次试验.收集的数据如下:| 零件个数x(个) | 1 | 2 | 3 | 4 |
| 加工时间y(小时) | 2 | 3 | 5 | 8 |
(Ⅱ)现需生产20件此零件,预测需用多长时间?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$x)
分析 (Ⅰ)分别求出$\overline{x}$,$\overline{y}$,代入公式计算即可;(Ⅱ)将x=20代入$\widehat{y}$=2x-0.5,计算即可.
解答 解:(Ⅰ)$\overline x$=$\frac{1+2+3+4}{4}$=2.5,$\overline{y}$=$\frac{2+3+5+8}{4}$=4.5,…(2分)
$\frac{{{\sum_{i=1}^{4}x}_{i}y}_{i}-4\overline{x}\overline{y}}{{{\sum_{i=1}^{4}x}_{i}}^{2}-{4\overline{x}}^{2}}$=$\frac{(2+6+15+32)-4×2.5×4.5}{(1+4+9+16)-4×2.5×2.5}$=2,…(5分)
$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=4.5-2×2.5=-0.5,…(7分)
所以$\widehat{y}$=2x-0.5.…(8分)
(Ⅱ)因为$\widehat{y}$=2×20-0.5=39.5(小时),…(9分)
所以生产20件此零件,预测需用39.5小时.…(10分)
点评 本题考查了线性规划问题,考查数据的处理,是一道基础题.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
20.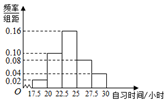 某中学调查200名学生每周晚自习时间(单位,小时),制成了如图所示频率分布直方图,其中自习时间的范围为[17.5,30],根据直方图,这200名学生每周自习时间不少于22.5小时的人数是140.
某中学调查200名学生每周晚自习时间(单位,小时),制成了如图所示频率分布直方图,其中自习时间的范围为[17.5,30],根据直方图,这200名学生每周自习时间不少于22.5小时的人数是140.
 某中学调查200名学生每周晚自习时间(单位,小时),制成了如图所示频率分布直方图,其中自习时间的范围为[17.5,30],根据直方图,这200名学生每周自习时间不少于22.5小时的人数是140.
某中学调查200名学生每周晚自习时间(单位,小时),制成了如图所示频率分布直方图,其中自习时间的范围为[17.5,30],根据直方图,这200名学生每周自习时间不少于22.5小时的人数是140.
10.已知抛物线x2=-2y的一条弦AB的中点坐标为(-1,-5),则这条弦AB所在的直线方程是( )
| A. | y=x-4 | B. | y=2x-3 | C. | y=-x-6 | D. | y=3x-2 |
15.已知集合A={-2,-1,0,1,2},集合B={x|x2≤1},A∩B=( )
| A. | {-2,-1,0,1} | B. | {-1,1} | C. | {-1,0} | D. | {-1,0,1} |