题目内容
20．某单位有500位职工，其中35岁以下的有125人，35～49岁的有280人，50岁以上的有95人，为了了解职工的健康状态，采用分层抽样的方法抽取一个容量为100的样本，需抽取35岁以下职工人数为25．分析 分层抽样应按各层所占的比例从总体中抽取，即可得出结论．
解答 解：分层抽样应按各层所占的比例从总体中抽取．
∵35岁以下的有125人，35～49岁的有280人，50岁以上的有95人，共抽出100人，
∴需抽取35岁以下职工人数为$\frac{125}{500}×100$=25人．
故答案为25．
点评 本题主要考查分层抽样，分层抽样的优点是：使样本具有较强的代表性，并且抽样过程中可综合选用各种抽样方法，因此分层抽样是一种实用、操作性强、应用比较广泛的抽样方法．
练习册系列答案
相关题目
10．已知抛物线x2=-2y的一条弦AB的中点坐标为（-1，-5），则这条弦AB所在的直线方程是（ ）
| A． | y=x-4 | B． | y=2x-3 | C． | y=-x-6 | D． | y=3x-2 |
11．已知直角坐标系中点A（0，1），向量$\overrightarrow{AB}=（-4，-3），\overrightarrow{BC}=（-7，-4）$，则点C的坐标为（ ）
| A． | （11，8） | B． | （3，2） | C． | （-11，-6） | D． | （-3，0） |
8．设函数f（x）=ex（3x-1）-ax+a，其中a＜1，若有且只有一个整数x0使得f（x0）≤0，则a的取值范围是（ ）
| A． | $（\frac{2}{e}，\frac{3}{4}）$ | B． | $[\frac{2}{e}，\frac{3}{4}）$ | C． | $（\frac{2}{e}，1）$ | D． | $[\frac{2}{e}，1）$ |
15．已知集合A={-2，-1，0，1，2}，集合B={x|x2≤1}，A∩B=（ ）
| A． | {-2，-1，0，1} | B． | {-1，1} | C． | {-1，0} | D． | {-1，0，1} |
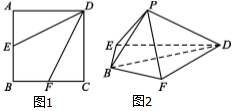如图，在边长为2的正方形ABCD中，点E，F分别是AB，BC的中点，将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于P．
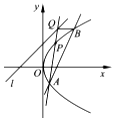已知直线l的方程为y=x+2，点P是抛物线y2=4x上到直线l距离最小的点，点A是抛物线上异于点P的点，直线AP与直线l交于点Q，过点Q与x轴平行的直线与抛物线y2=4x交于点B．
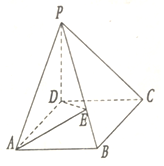如图在棱锥P-ABCD中，ABCD为矩形，PD⊥面ABCD，PB=2，PB与面PCD成45°角，PB与面ABD成30°角．