题目内容
设函数f(x)=(x2+ax-2a-3)e3-x
(1)求函数的单调区间;
(2)对于两个函数y=h(x)和y=r(x)及区间[m,n],若存在x1∈[m,n],x2∈[m,n]使得|h(x1)-r(x2)|<1成立,则称区间是函数y=h(x)和y=r(x)的“非疏远区间”,a>0,g(x)=x2+ax+a2-a+7,若区间[0,4]是函数y=f(x)和y=g(x)的“非疏远区间”,求a的取值范围.
(1)求函数的单调区间;
(2)对于两个函数y=h(x)和y=r(x)及区间[m,n],若存在x1∈[m,n],x2∈[m,n]使得|h(x1)-r(x2)|<1成立,则称区间是函数y=h(x)和y=r(x)的“非疏远区间”,a>0,g(x)=x2+ax+a2-a+7,若区间[0,4]是函数y=f(x)和y=g(x)的“非疏远区间”,求a的取值范围.
考点:利用导数研究函数的单调性,函数单调性的性质
专题:函数的性质及应用
分析:(1)先求导函数,利用x=3是函数f(x)的极值点,可得-(a+1)≠3即a≠-4,进而分a>-4与a<-4,分类讨论,研究函数的单调性;
(2)分别求出gmin(x)与fmax(x),再将问题等价转化为:若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1,只要gmin(x)-fmax(x)<1即可,从而解不等式,即可求出a的取值范围.
(2)分别求出gmin(x)与fmax(x),再将问题等价转化为:若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1,只要gmin(x)-fmax(x)<1即可,从而解不等式,即可求出a的取值范围.
解答:
解:(1)f′(x)=(2x+a)e3-x+(x2+ax-2a-3)(-1)e3-x
=[-x2+(2-a)x+3a+3]e3-x=-[x2+(a-2)x-3(a+1)]e3-x
=-(x-3)[x+(a+1)]e3-x…(3分)
∵x=3是函数f(x)的极值点
∴-(a+1)≠3即a≠-4
(i)当-(a+1)<3即a>-4时
当x∈(-∞,-a-1]和[3,+∞)时,f′(x)≤0,f(x)单调递减
当x∈(-a-1,3)时,f′(x)>0,f(x)单调递增.…(5分)
(ii)当-(a+1)>3即a<-4时
当x∈(-∞,3]和[-a-1,+∞)时,f′(x)≤0,f(x)单调递减
当x∈(3,-a-1)时,f′(x)>0,f(x)单调递增.…(7分)
(2)∵a>0,∴-(a+1)<0
∴当x∈[0,3]时f(x)单调递增,当x∈[3,4]时f(x)单调递减
∴当x∈[0,4]时,fmax(x)=f(3)=a+6,
∵g′(x)=2x+2a,
∴g(x)在x∈[0,4]时是增函数,
∴gmin(x)=g(0)=a2-a+7,
又∵a2-a+7-a-6=(a-1)2≥0,
∴gmin(x)≥fmax(x),
∴当x∈[0,4]时,g(x)≥f(x)恒成立.
∴若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1
只要gmin(x)-fmax(x)<1即可,
即a2-2a+1<1,解得:0<a<2,
∴a的范围是(0,2).
=[-x2+(2-a)x+3a+3]e3-x=-[x2+(a-2)x-3(a+1)]e3-x
=-(x-3)[x+(a+1)]e3-x…(3分)
∵x=3是函数f(x)的极值点
∴-(a+1)≠3即a≠-4
(i)当-(a+1)<3即a>-4时
当x∈(-∞,-a-1]和[3,+∞)时,f′(x)≤0,f(x)单调递减
当x∈(-a-1,3)时,f′(x)>0,f(x)单调递增.…(5分)
(ii)当-(a+1)>3即a<-4时
当x∈(-∞,3]和[-a-1,+∞)时,f′(x)≤0,f(x)单调递减
当x∈(3,-a-1)时,f′(x)>0,f(x)单调递增.…(7分)
(2)∵a>0,∴-(a+1)<0
∴当x∈[0,3]时f(x)单调递增,当x∈[3,4]时f(x)单调递减
∴当x∈[0,4]时,fmax(x)=f(3)=a+6,
∵g′(x)=2x+2a,
∴g(x)在x∈[0,4]时是增函数,
∴gmin(x)=g(0)=a2-a+7,
又∵a2-a+7-a-6=(a-1)2≥0,
∴gmin(x)≥fmax(x),
∴当x∈[0,4]时,g(x)≥f(x)恒成立.
∴若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1
只要gmin(x)-fmax(x)<1即可,
即a2-2a+1<1,解得:0<a<2,
∴a的范围是(0,2).
点评:本题以函数的极值为载体,考查导数的运用,考查利用导数求函数的单调区间,同时考查学生分析解决问题的能力

练习册系列答案
 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
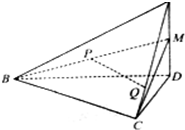 在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,∠DBC=30°,AD=2,BD=2
在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,∠DBC=30°,AD=2,BD=2 如图,四棱锥P-ABCD中,PA⊥AD,AD=
如图,四棱锥P-ABCD中,PA⊥AD,AD=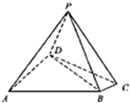 如图,四棱锥P-ABCD,∠DAB=90°,BC⊥CD,∠CDB=30°,且PA=PB=PD=AB=AD=
如图,四棱锥P-ABCD,∠DAB=90°,BC⊥CD,∠CDB=30°,且PA=PB=PD=AB=AD=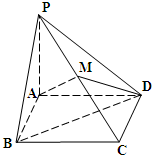 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,点M是棱PC的中点,AM⊥平面PBD.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,点M是棱PC的中点,AM⊥平面PBD.