题目内容
设函数f(x)=lnx-cx(c∈R).
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若f(x)≤x2恒成立,求c的取值范围;
(Ⅲ)设f(x)有两个相异零点x1,x2,求证x1•x2>e2.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若f(x)≤x2恒成立,求c的取值范围;
(Ⅲ)设f(x)有两个相异零点x1,x2,求证x1•x2>e2.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)求函数的导数,根据函数单调性和导数之间的关系即可得到结论.
(Ⅱ)将不等式f(x)≤x2恒成立进行转化为求函数的最值问题,利用导数即可求c的取值范围;
(Ⅲ)利用函数零点的性质,结合函数单调性和导数之间的关系,进行转化即可证明不等式.
(Ⅱ)将不等式f(x)≤x2恒成立进行转化为求函数的最值问题,利用导数即可求c的取值范围;
(Ⅲ)利用函数零点的性质,结合函数单调性和导数之间的关系,进行转化即可证明不等式.
解答:
解:(Ⅰ)∵f(x)=lnx-cx,∴x>0,
f′(x)=
-c=
.
当c≤0时,f(x)单调增区间为(0,+∞).
当c>0时,f(x)单调增区间为(0,
),f(x)单调减区间为(
,+∞)
( II)∵f(x)≤x2,∴lnx-cx≤x2,
∴c≥
-x.
设g(x)=
-x,∴g′(x)=
,
∴g(x)在(0,1)单调递增,在(1,+∞)单调递减.
∴g(x)的最大值为g(1)=-1,∴c≥-1.
(III)∵f(x)有两个相异零点,∴设lnx1=cx1,lnx2=cx2,①
即lnx1-lnx2=c(x1-x2),
∴
=c,②
而x1•x2>e2,等价于:lnx1+lnx2>2,即c(x1+x2)>2,③
由①②③得:
(x1+x2)>2,
不妨设x1>x2>0,则t=
>1,
上式转化为:lnt>
,t>1
设H(t)=lnt-
,t>1,
则H′(t)=
>0,
故函数H(t)是(1,+∞)上的增函数,
∴H(t)>H(1)=0,
即不等式lnt>
成立,
故所证不等式x1•x2>e2成立.
f′(x)=
| 1 |
| x |
| 1-cx |
| x |
当c≤0时,f(x)单调增区间为(0,+∞).
当c>0时,f(x)单调增区间为(0,
| 1 |
| c |
| 1 |
| c |
( II)∵f(x)≤x2,∴lnx-cx≤x2,
∴c≥
| lnx |
| x |
设g(x)=
| lnx |
| x |
| 1-lnx-x2 |
| x2 |
∴g(x)在(0,1)单调递增,在(1,+∞)单调递减.
∴g(x)的最大值为g(1)=-1,∴c≥-1.
(III)∵f(x)有两个相异零点,∴设lnx1=cx1,lnx2=cx2,①
即lnx1-lnx2=c(x1-x2),
∴
| lnx1-lnx |
| x1-x2 |
而x1•x2>e2,等价于:lnx1+lnx2>2,即c(x1+x2)>2,③
由①②③得:
| lnx1-lnx2 |
| x1-x2 |
不妨设x1>x2>0,则t=
| x1 |
| x2 |
上式转化为:lnt>
| 2(t-1) |
| t+1 |
设H(t)=lnt-
| 2(t-1) |
| t+1 |
则H′(t)=
| (t-1)2 |
| t(t+1)2 |
故函数H(t)是(1,+∞)上的增函数,
∴H(t)>H(1)=0,
即不等式lnt>
| 2(t-1) |
| t+1 |
故所证不等式x1•x2>e2成立.
点评:本题主要考查函数单调性和导数之间的关系和应用,以及利用函数的导数研究函数的最值和零点问题,综合性较强,运算量较大.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
等差数列{an}中,a4=39,a8=33,则a16=( )
| A、30 | B、27 | C、24 | D、21 |
设m∈N*,且m<15,则(15-m)(16-m)…(20-m)等于( )
A、A
| ||
B、A
| ||
C、A
| ||
D、A
|
复数z和它的共轭复数
在复平面内所对应的点关于( )对称.
. |
| z |
| A、原点 | B、实轴 |
| C、虚轴 | D、直线x=y |
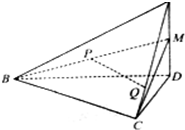 在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,∠DBC=30°,AD=2,BD=2
在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,∠DBC=30°,AD=2,BD=2