题目内容
19.已知双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点为F1(0,-c)(c>0),离心率为e,过F1平行于双曲线渐近线的直线与圆x2+y2=c2交于另一点P,且点P在抛物线x2=4cy上,则e2=( )| A. | $\frac{\sqrt{5}+2}{2}$ | B. | $\frac{\sqrt{5}+2}{3}$ | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{\sqrt{5}+1}{3}$ |
分析 设双曲线的一条渐近线方程,设P(x,y),运用点P满足抛物线的方程和圆的方程,解得P的坐标(用c表示),
再由两直线平行的条件,即可得到a,b的关系,由离心率公式可得所求值.
解答 解:设P(x,y),
双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1的一条渐近线方程为y=$\frac{a}{b}$x,
由题意可得$\left\{\begin{array}{l}{{x}^{2}=4cy①}\\{{x}^{2}+{y}^{2}={c}^{2}②}\\{\frac{y+c}{x}=\frac{a}{b}③}\end{array}\right.$
将①代入②得y2+4cy-c2=0,
则y=-2c±$\sqrt{5}$c,
即y=($\sqrt{5}$-2)c,(负值舍去),
代入③,即x=$\frac{(\sqrt{5}-1)bc}{a}$,
再将x代入①得,$\frac{(6-2\sqrt{5}){b}^{2}{c}^{2}}{{a}^{2}}$=4($\sqrt{5}$-2)c2,
即为b2=c2-a2=$\frac{2(\sqrt{5}-2)}{3-\sqrt{5}}$a2,
即c2=$\frac{1+\sqrt{5}}{2}$a2,
由e=$\frac{c}{a}$,
可得e2=$\frac{\sqrt{5}+1}{2}$.
故选:C.
点评 本题考查双曲线的性质,抛物线的方程的运用,运用双曲线的渐近线方程、以及直线平行的性质是解题的关键,考查化简整理的运算能力,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
9.角α的终边上一点的坐标为$(2sin\frac{2π}{3},2cos\frac{2π}{3})$,则sinα等于( )
| A. | $-\frac{1}{2}$ | B. | -1 | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
10.已知双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左,右顶点为A,B,点M在E上,△ABM为等腰三角形,且顶角θ满足cosθ=-$\frac{1}{3}$,则E的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
4.已知函数f(x)=$\left\{\begin{array}{l}{2x,(x≤\frac{1}{2})}\\{2-2x,(x>\frac{1}{2})}\end{array}\right.$,则函数$\underset{\underbrace{f(f(…f(x)…))}}{2015}$在[0,1]上的图象总长( )
| A. | 8060 | B. | 4030 | C. | 2015$\sqrt{5}$ | D. | $\sqrt{{2^{4030}}+1}$ |
9.执行下面的程序框图,如果输入的t=0.01,则输出的n=( )


| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
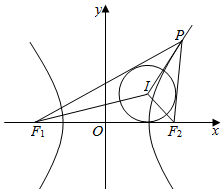 已知点P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)右支上一点,F1,F2分别为双曲线的左右焦点,且|F1F2|=$\frac{{b}^{2}}{a}$,I为△PF1F2的内心,若λS${\;}_{△IP{F}_{1}}$=λS${\;}_{△IP{F}_{2}}$+S${\;}_{△I{F}_{1}{F}_{2}}$成立,则λ的值为$\sqrt{2}$-1.
已知点P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)右支上一点,F1,F2分别为双曲线的左右焦点,且|F1F2|=$\frac{{b}^{2}}{a}$,I为△PF1F2的内心,若λS${\;}_{△IP{F}_{1}}$=λS${\;}_{△IP{F}_{2}}$+S${\;}_{△I{F}_{1}{F}_{2}}$成立,则λ的值为$\sqrt{2}$-1.