题目内容
9．执行下面的程序框图，如果输入的t=0.01，则输出的n=（ ）
| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
分析 由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量n的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．
解答 解：第一次执行循环体后，S=$\frac{1}{2}$，m=$\frac{1}{4}$，n=1，不满足退出循环的条件；
再次执行循环体后，S=$\frac{1}{4}$，m=$\frac{1}{8}$，n=2，不满足退出循环的条件；
再次执行循环体后，S=$\frac{1}{8}$，m=$\frac{1}{16}$，n=3，不满足退出循环的条件；
再次执行循环体后，S=$\frac{1}{16}$，m=$\frac{1}{32}$，n=4，不满足退出循环的条件；
再次执行循环体后，S=$\frac{1}{32}$，m=$\frac{1}{64}$，n=5，不满足退出循环的条件；
再次执行循环体后，S=$\frac{1}{64}$，m=$\frac{1}{128}$，n=6，不满足退出循环的条件；
再次执行循环体后，S=$\frac{1}{128}$，m=$\frac{1}{256}$，n=7，满足退出循环的条件；
故输出的n值为7，
故选：C
点评 本题考查的知识点是程序框图，当循环的次数不多，或有规律时，常采用模拟循环的方法解答，属于基础题．
练习册系列答案
相关题目
19．已知双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一个焦点为F1（0，-c）（c＞0），离心率为e，过F1平行于双曲线渐近线的直线与圆x2+y2=c2交于另一点P，且点P在抛物线x2=4cy上，则e2=（ ）
| A． | $\frac{\sqrt{5}+2}{2}$ | B． | $\frac{\sqrt{5}+2}{3}$ | C． | $\frac{\sqrt{5}+1}{2}$ | D． | $\frac{\sqrt{5}+1}{3}$ |
14．执行如图所示的程序框图，则输出S的值是（ ）
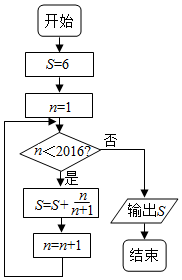
| A． | 336 | B． | $\frac{1}{336}$ | C． | 2016 | D． | $\frac{1}{2016}$ |
1．2004 年世界卫生组织、联合国儿童基金会等机构将青蒿素作为一线抗疟药品推广．2015 年12 月10 日，我国科学家屠呦呦教授由于在发现青蒿素和治疗疟疾的疗法上的贡献获得诺贝尔医学奖．目前，国内青蒿人工种植发展迅速．
某农科所为了深入研究海拔因素对青蒿素产量的影响，在山上和山下的试验田中分别种植了100 株青蒿进行对比试验．现在从山上和山下的试验田中各随机选取了4株青蒿作为样本，每株提取的青蒿素产量（单位：克）如表所示：
（Ⅰ）根据样本数据，试估计山下试验田青蒿素的总产量；
（Ⅱ）记山上与山下两块试验田单株青蒿素产量的方差分别为$s_1^2$，$s_2^2$，根据样本数据，试估计$s_1^2$与$s_2^2$的大小关系（只需写出结论）；
（Ⅲ）从样本中的山上与山下青蒿中各随机选取1 株，记这2 株的产量总和为ξ，求随机变量ξ的分布列和数学期望．
某农科所为了深入研究海拔因素对青蒿素产量的影响，在山上和山下的试验田中分别种植了100 株青蒿进行对比试验．现在从山上和山下的试验田中各随机选取了4株青蒿作为样本，每株提取的青蒿素产量（单位：克）如表所示：
| 编号 位置 | ① | ② | ③ | ④ |
| 山上 | 5.0 | 3.8 | 3.6 | 3.6 |
| 山下 | 3.6 | 4.4 | 4.4 | 3.6 |
（Ⅱ）记山上与山下两块试验田单株青蒿素产量的方差分别为$s_1^2$，$s_2^2$，根据样本数据，试估计$s_1^2$与$s_2^2$的大小关系（只需写出结论）；
（Ⅲ）从样本中的山上与山下青蒿中各随机选取1 株，记这2 株的产量总和为ξ，求随机变量ξ的分布列和数学期望．