题目内容
10.已知双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左,右顶点为A,B,点M在E上,△ABM为等腰三角形,且顶角θ满足cosθ=-$\frac{1}{3}$,则E的离心率为( )| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
分析 根据△ABM是顶角θ满足cosθ=-$\frac{1}{3}$的等腰三角形,得出|BM|=|AB|=2a,cos∠MBx=$\frac{1}{3}$,进而求出点M的坐标,再将点M代入双曲线方程即可求出离心率.
解答 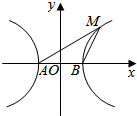 解:不妨取点M在第一象限,如右图:
解:不妨取点M在第一象限,如右图:
∵△ABM是顶角θ满足cosθ=-$\frac{1}{3}$的等腰三角形,
∴|BM|=|AB|=2a,cos∠MBx=$\frac{1}{3}$,
∴点M的坐标为(a+$\frac{2a}{3}$,2a•$\frac{2\sqrt{2}}{3}$),即($\frac{5a}{3}$,$\frac{4\sqrt{2}a}{3}$),
又∵点M在双曲线E上,
∴将M坐标代入坐标得$\frac{25}{9}$-$\frac{32{a}^{2}}{9{b}^{2}}$=1,
整理上式得,b2=2a2,
而c2=a2+b2=3a2,
∴e2=$\frac{{c}^{2}}{{a}^{2}}$=$\sqrt{3}$,
因此e=$\sqrt{3}$,
故选:C.
点评 本题主要考查了双曲线的简单几何性质:离心率,灵活运用三角函数的定义是解决本题的关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知${C}_{n}^{0}$,${C}_{n}^{1}$,${C}_{n}^{2}$,…,${C}_{n}^{n}$中最大值的项只有${C}_{n}^{5}$,则${C}_{n}^{0}$+${C}_{n}^{1}$+${C}_{n}^{2}$+…+${C}_{n}^{n}$=( )
| A. | 25 | B. | 28 | C. | 29 | D. | 210 |
5.若双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)经过等腰梯形ABCD的上底的两个顶点C、D,下底的两个顶点A、B分别为双曲线的左、右焦点,对角线AC与双曲线的左支交于点E,且3|AE|=2|EC|,|AB|=2|CD|,则该双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
19.已知双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点为F1(0,-c)(c>0),离心率为e,过F1平行于双曲线渐近线的直线与圆x2+y2=c2交于另一点P,且点P在抛物线x2=4cy上,则e2=( )
| A. | $\frac{\sqrt{5}+2}{2}$ | B. | $\frac{\sqrt{5}+2}{3}$ | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{\sqrt{5}+1}{3}$ |