题目内容
如图，AB是圆O的直径，过A、B的两条弦AC和BD相交于点P，若圆O的半径是2，那么AC•AP+BD•BP的值等于考点：与圆有关的比例线段
专题：选作题,立体几何
分析：连接AD、BC，过P作PM⊥AB，则∠ADB=∠AMP=90°，可得点D、M在以AP为直径的圆上；M、C在以BP为直径的圆上．由割线定理，即可得出结论．
解答：
解：连接AD、BC，过P作PM⊥AB，则∠ADB=∠AMP=90°，
∴点D、M在以AP为直径的圆上；
同理：M、C在以BP为直径的圆上．
由割线定理得：AP•AC=AM•AB，BP•BD=BM•BA，
∴AP•AC+BP•BD=AM•AB+BM•AB=AB•（AM+BM）=AB2=16．
故答案为：16．
解：连接AD、BC，过P作PM⊥AB，则∠ADB=∠AMP=90°，∴点D、M在以AP为直径的圆上；
同理：M、C在以BP为直径的圆上．
由割线定理得：AP•AC=AM•AB，BP•BD=BM•BA，
∴AP•AC+BP•BD=AM•AB+BM•AB=AB•（AM+BM）=AB2=16．
故答案为：16．
点评：本题考查了割线定理，考查学生分析解决问题的能力，正确运用割线定理是关键．
练习册系列答案
相关题目
如图，PC切圆O于点C，割线PAB经过圆心O，弦CD⊥AB于点E，已知圆O的半径为3，PA=2，则CE=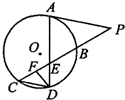
如图，A是⊙O上的点，PC与⊙O相交于B、C两点，点D在⊙O上，CD∥AP，AD与BC交于E，F为CE上的点，若∠EDF=∠P，AE=12，ED=6，EF=4，则PB=
已知数列{an}为等差数列，Sn为{an}的前n项和，且Sn=n2，则a10=（ ）
| A、17 | B、18 | C、19 | D、20 |