题目内容
下面给出的命题中:
①“m=-2”是直线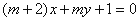 与“直线
与“直线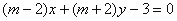 相互垂直”的必要不充分条件;
相互垂直”的必要不充分条件;
②已知函数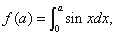 则
则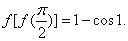
③已知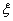 服从正态分布
服从正态分布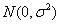 ,且
,且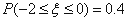 ,则
,则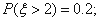
④已知⊙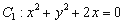 ,⊙
,⊙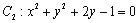 ,则这两圆恰有2条公切线;
,则这两圆恰有2条公切线;
⑤将函数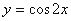 的图象向右平移
的图象向右平移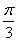 个单位,得到函数
个单位,得到函数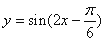 的图象。
的图象。
其中是真命题的有 _____________。(填序号)
②④⑤ 解析:①m=-2时,直线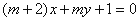 即
即 ,直线
,直线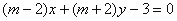 即
即 ,此时两直线垂直,故m=-2是两直线垂直的充分条件,故①错误;
,此时两直线垂直,故m=-2是两直线垂直的充分条件,故①错误;
②函数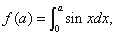 =
= ,
, ,则
,则 ,故②正确;
,故②正确;
③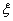 服从正态分布
服从正态分布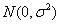 ,且
,且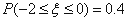 ,
,
则 ,故③错误;
,故③错误;
④⊙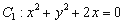 和⊙
和⊙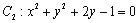 的圆心分别为:
的圆心分别为: ,半径分别为:
,半径分别为: ,所以两圆心的距离为
,所以两圆心的距离为 ,半径和为
,半径和为 ,差的绝对值为
,差的绝对值为 ,所以两圆相交,恰有2条公切线,故④正确;
,所以两圆相交,恰有2条公切线,故④正确;
⑤将函数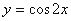 的图象向右平移
的图象向右平移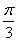 个单位,得到函数
个单位,得到函数 故⑤正确,
故⑤正确,
故答案为:②④⑤
【思路点拨】将m=-2代入直线中化简可判断①;利用定积分求出函数 的解析式即可判断②;根据正态曲线的对称性可判断③;判断出两圆的位置关系可得到④的真假;利用函数图像的平移及诱导公式可判断出⑤。
的解析式即可判断②;根据正态曲线的对称性可判断③;判断出两圆的位置关系可得到④的真假;利用函数图像的平移及诱导公式可判断出⑤。

练习册系列答案
相关题目
 是首项为
是首项为 ,公差为
,公差为 的等差数列,若数列
的等差数列,若数列 是等比数列,则其公比为( )
是等比数列,则其公比为( )






 的前
的前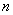 项和为
项和为 ,若
,若 (
( ),则
),则 .
. 满足
满足 ,则目标函数
,则目标函数 -1的最大值为
-1的最大值为 D.
D. 
 的边长是3,
的边长是3, 是
是 上的点,BD=1,则
上的点,BD=1,则 =
= B.
B. C.
C. D.
D.
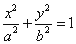 (a>b>0)的左、右焦点,且离心率为
(a>b>0)的左、右焦点,且离心率为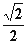 ,点
,点 椭圆C上。
椭圆C上。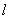 与椭圆C交于不同的两点M、N,使直线
与椭圆C交于不同的两点M、N,使直线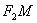 与
与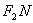 的倾斜角互补,且直线
的倾斜角互补,且直线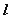 是否恒过定点,若存在,求出该定点的坐标;若不存在,说明理由。
是否恒过定点,若存在,求出该定点的坐标;若不存在,说明理由。 的倾斜角是
的倾斜角是 ,则
,则 (结果用反三角函数值表示).
(结果用反三角函数值表示).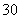 名,高二学生有
名,高二学生有 名,现用分层抽样的方
名,现用分层抽样的方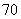 名学生中抽取一个样本,已知在高一学生中抽取了
名学生中抽取一个样本,已知在高一学生中抽取了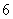 人,则在高二学生中应抽
人,则在高二学生中应抽 是方向分别与
是方向分别与 轴和
轴和 轴正方向相同的两个基本单位向量,则平面向量
轴正方向相同的两个基本单位向量,则平面向量 的模等于 .
的模等于 .