题目内容
已知F1、F2分别为椭圆C: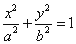 (a>b>0)的左、右焦点,且离心率为
(a>b>0)的左、右焦点,且离心率为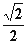 ,点
,点 椭圆C上。
椭圆C上。
(1)求椭圆C的方程;
(2)是否存在斜率为k的直线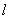 与椭圆C交于不同的两点M、N,使直线
与椭圆C交于不同的两点M、N,使直线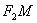 与
与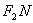 的倾斜角互补,且直线
的倾斜角互补,且直线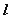 是否恒过定点,若存在,求出该定点的坐标;若不存在,说明理由。
是否恒过定点,若存在,求出该定点的坐标;若不存在,说明理由。
解:(1) 由已知得: ,
, ,结合
,结合 ,可解得:
,可解得:  ,
,

由已知直线F2M与F2N的倾斜角互补,
得
化简,得

整理得
直线MN的方程为 ,
,
因此直线MN过定点,该定点的坐标为(2,0)
【思路点拨】(1)由已知条件可得出两个关于 的方程,结合
的方程,结合 ,解得
,解得 的值,即可得到椭圆的方程;
的值,即可得到椭圆的方程;
(2)设出直线的方程,与椭圆方程联立,消去 ,得到一个关于
,得到一个关于 的一元二次方程,再设出点
的一元二次方程,再设出点 的坐标,利用韦达定理得出坐标的关系,然后利用直线F2M与F2N的倾斜角互补,列出直线的斜率
的坐标,利用韦达定理得出坐标的关系,然后利用直线F2M与F2N的倾斜角互补,列出直线的斜率 和截距
和截距 的等式,化简即可得结论。
的等式,化简即可得结论。

练习册系列答案
相关题目
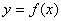 的定义域为
的定义域为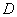 ,若对于任意
,若对于任意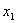 、
、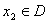 ,当
,当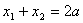 时,恒有
时,恒有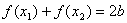 ,则称点
,则称点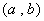 为函数
为函数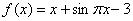 的某一个对称中心,并利用对称中心的上述定义,可得到
的某一个对称中心,并利用对称中心的上述定义,可得到 的值为……………………( )
的值为……………………( )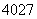 B.
B.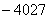 C.
C.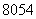 D.
D.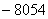
 是递增的等差数列,且
是递增的等差数列,且 ,
, .
.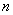 项和
项和 的最小值;
的最小值; 的前
的前 .
.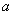 为如图所示的程序框图输出的结果,则二项式
为如图所示的程序框图输出的结果,则二项式 的展开式中常数项是
的展开式中常数项是 A. -20 B.
A. -20 B.  C. -192 D. -160
C. -192 D. -160 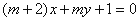 与“直线
与“直线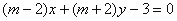 相互垂直”的必要不充分条件;
相互垂直”的必要不充分条件;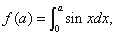 则
则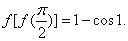
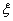 服从正态分布
服从正态分布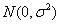 ,且
,且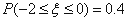 ,则
,则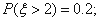
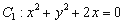 ,⊙
,⊙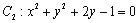 ,则这两圆恰有2条公切线;
,则这两圆恰有2条公切线;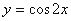 的图象向右平移
的图象向右平移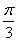 个单位,得到函数
个单位,得到函数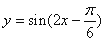 的图象。
的图象。 到两条直线
到两条直线 与
与 的距离之和等于
的距离之和等于 ,则
,则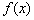 满足:集合
满足:集合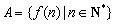 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数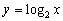 ;②
;②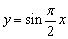 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)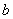 ,函数
,函数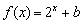 不是等比源函数;
不是等比源函数;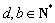 ,函数
,函数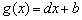 都是等比源函数.
都是等比源函数.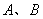 是互斥事件,若
是互斥事件,若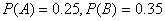 ,则
,则 ;
;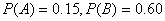 ,则
,则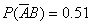 (
(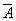 表示事件
表示事件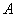 的对立事件);
的对立事件);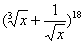 的二项展开式中,共有4个有理项.
的二项展开式中,共有4个有理项. ,则异面直线
,则异面直线 与
与 所成角余弦值为 .
所成角余弦值为 .