题目内容
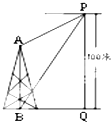
在高为100米的山顶P处，测得山下一塔顶A和塔底B的俯角分别为30°和60°，则塔AB的高为 米．
考点：解三角形的实际应用
专题：计算题,应用题,解三角形
分析：由题意，设塔高为h米，由题知∠APQ=60°，∠PBQ=30°，则∠APB=30°，在△PBQ，△APB中求解即可．
解答：
解：如图所示，设塔高为h米，由题知∠APQ=60°，∠PBQ=30°，则∠APB=30°，
在△PBQ中，
PB=
=
，
则在△APB中，由正弦定理得，
=
，
解得h=
（米）．
故答案为：
．
在△PBQ中，
PB=
| 100 |
| cos30° |
| 200 | ||
|
则在△APB中，由正弦定理得，
| h |
| sin30° |
| PB |
| sin120° |
解得h=
| 200 |
| 3 |
故答案为：
| 200 |
| 3 |
点评：本题考查了解三角形在实际问题中的应用，属于中档题．
练习册系列答案
相关题目
已知集合U={x|x＞0}，集合A={x∈U|1-
≥0}，则集合CUA=（ ）
| 1 |
| x |
| A、x|x≥1} |
| B、x|x≥1} |
| C、{x|x≥1} |
| D、{x|0＜x＜1} |
若集合A={x|lgx≤0}，B={x|2x≤1}，全集U=R，则∁U（A∪B）=（ ）
| A、（-∞，1） |
| B、（1，+∞） |
| C、（-∞，1] |
| D、[1，+∞） |
已知函数f（x）=x2-2ax-b2+16．