题目内容
 已知函数f(x)=x2-2ax-b2+16.
已知函数f(x)=x2-2ax-b2+16.(1)若a,b是一枚骰子投掷两次所得到的点数,求函数f(x)无零点的概率;
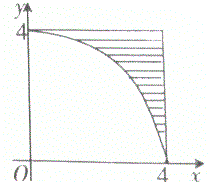
(2)如图,在边长为4的正方形内均匀地取n个点Pi(xi,yi),若a=xi,b=yi(i∈{1,2,…,n}),统计出使函数f(x)有两个不相等零点的点Pi的个数为m,当n充分大时,求圆周率π的近似值(用m,n表示).
考点:几何概型
专题:概率与统计
分析:(1)由题意知本题是一个古典概型,试验发生包含的所有事件数是6×6,满足条件的是使得二次函数f(x)=x2-2ax-b2+16无零点,
即满足△=a2+b2<16,讨论当a为1、2、3、4、5、6时对应的b的值,得到满足条件的事件数,得到结果.
(2)由题意知本题是一个几何概型,试验发生包含的所有事件是正方形区域面积为4×4=16,满足条件的是使得二次函数f(x)=x2-2ax-b2+16有两个不相等零点即满足△=a2+b2>16,利用几何概型与古典概型概率关系得到m,n表示的π的等式,求出π.
即满足△=a2+b2<16,讨论当a为1、2、3、4、5、6时对应的b的值,得到满足条件的事件数,得到结果.
(2)由题意知本题是一个几何概型,试验发生包含的所有事件是正方形区域面积为4×4=16,满足条件的是使得二次函数f(x)=x2-2ax-b2+16有两个不相等零点即满足△=a2+b2>16,利用几何概型与古典概型概率关系得到m,n表示的π的等式,求出π.
解答:
解:(1)由题意知本题是一个古典概型,
试验发生包含的所有事件数是6×6=36,
满足条件的是使得二次函数f(x)=x2-2ax-b2+16无零点,
即满足△<0,
△=a2+b2<16,
共有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2)共有8个,
∴函数f(x)无零点的概率是
=
;
(2)由题意知本题是一个几何概型,
试验发生包含的所有事件是正方形区域面积为4×4=16,
满足条件的是使得二次函数f(x)=x2-2ax-b2+16有两个不相等零点
即满足△>0,即△=a2+b2>16,对应区域如图阴影部分,其面积为42-π×42×
=16-4π=m,
所以
=
,所以π=4(1-
).
试验发生包含的所有事件数是6×6=36,
满足条件的是使得二次函数f(x)=x2-2ax-b2+16无零点,
即满足△<0,
△=a2+b2<16,
共有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2)共有8个,
∴函数f(x)无零点的概率是
| 8 |
| 36 |
| 2 |
| 9 |
(2)由题意知本题是一个几何概型,
试验发生包含的所有事件是正方形区域面积为4×4=16,
满足条件的是使得二次函数f(x)=x2-2ax-b2+16有两个不相等零点
即满足△>0,即△=a2+b2>16,对应区域如图阴影部分,其面积为42-π×42×
| 1 |
| 4 |
所以
| m |
| n |
| 16-4π |
| 16 |
| m |
| n |
点评:本题考查了古典概型与几何概型的概率求法;古典概型要求能够列举出所有事件和发生事件的个数,本题可以列举出所有事件,概率问题同其他的知识点结合在一起,实际上是以概率问题为载体,本题主要考查函数零点的问题.

练习册系列答案
相关题目
“x<2”和“x2-x-2<0”的关系是( )
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |