题目内容
9．已知向量$\vec a$，$\vec b$的夹角为$\frac{π}{3}$，且$\vec a•（\vec a-\vec b）=1$，$|\vec a|=2$，则$|\vec b|$=3．分析 根据$＜\overrightarrow{a}，\overrightarrow{b}＞=\frac{π}{3}，|\overrightarrow{a}|=2$进行数量积的运算便可得出$\overrightarrow{a}•（\overrightarrow{a}-\overrightarrow{b}）=4-|\overrightarrow{b}|$，从而得出$4-|\overrightarrow{b}|=1$，这样便可求出$|\overrightarrow{b}|$的值．
解答 解：根据条件：
$\overrightarrow{a}•（\overrightarrow{a}-\overrightarrow{b}）={\overrightarrow{a}}^{2}-\overrightarrow{a}•\overrightarrow{b}$=$4-2|\overrightarrow{b}|•\frac{1}{2}=1$；
∴$|\overrightarrow{b}|=3$．
故答案为：3．
点评 考查向量夹角的概念，向量数量积的运算及计算公式．
练习册系列答案
相关题目
19．某班主任对全班50名学生进行了作业量多少的调查，根据列联表数据计算得到K2=5.059，因为P（K2≥5.024）=0.025，则认为“喜欢玩电脑游戏与认为作业量的多少有关系”的把握大约为（ ）
| A． | 2.5% | B． | 95% | C． | 97.5% | D． | 不具有相关性 |
4．某社区调查了老年大学全部48名学员参加书法班和演讲班的情况，数据如表：（单位：人）
（I）从该老年大学随机选1名学员，求该学员至少参加上述一个班的概率；
（II）在既参加书法班又参加演讲班的8名学员中，有5名男学员A1，A2，A3，A4，A5，3名女学员B1，B2，B3．现从这5名男学员和3名女学员中各随机选1人，求A1被选中且B1未被选中的概率．
| 参加书法班 | 未参加书法班 | |
| 参加演讲班 | 8 | 5 |
| 未参加演讲班 | 2 | 33 |
（II）在既参加书法班又参加演讲班的8名学员中，有5名男学员A1，A2，A3，A4，A5，3名女学员B1，B2，B3．现从这5名男学员和3名女学员中各随机选1人，求A1被选中且B1未被选中的概率．
14．已知f'（x）为定义在$（{0，\frac{π}{2}}）$上的函数f（x）的导函数，且cosx•f（x）＜f'（x）•sinx在$（{0，\frac{π}{2}}）$上恒成立，则（ ）
| A． | $\sqrt{3}f（{\frac{π}{4}}）＞\sqrt{2}f（{\frac{π}{3}}）$ | B． | $\sqrt{2}f（{\frac{π}{6}}）＞f（{\frac{π}{4}}）$ | C． | $\sqrt{3}f（{\frac{π}{6}}）＜f（{\frac{π}{3}}）$ | D． | $f（1）＜2f（{\frac{π}{6}}）sin1$ |
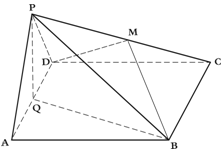如图示，边长为4的正方形ABCD与正三角形ADP所在平面互相垂直，M、Q分别是PC，AD的中点．