题目内容
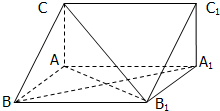 直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB=
直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB=| π |
| 2 |
(Ⅰ)证明:BA1⊥平面CAB1;
(Ⅱ)已知AB=2,BC=
| 5 |
考点:直线与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(I)连接AB1,根据ABC-A1B1C1是直三棱柱,得到平面ABC⊥平面ABB1A1,结合AC⊥AB,可得AC⊥平面ABB1A1,从而有AC⊥BA1,再在正方形ABB1A1中得到AB1⊥BA1,最后根据线面垂直的判定定理,得到BA1⊥平面ACB1,所以CB1⊥BA1;
(II)在Rt△ABC中,利用勾股定理,得到AC=1,又因为直三棱柱ABC-A1B1C1中,A1C1=AC=1且AC⊥平面ABB1A1,得到A1C1是三棱锥C1-ABA1的高,且它的长度为1.再根据正方形ABB1A1面积得到△ABA1的面积,最后根据锥体体积公式,得到三棱锥C1-ABA1的体积.
(II)在Rt△ABC中,利用勾股定理,得到AC=1,又因为直三棱柱ABC-A1B1C1中,A1C1=AC=1且AC⊥平面ABB1A1,得到A1C1是三棱锥C1-ABA1的高,且它的长度为1.再根据正方形ABB1A1面积得到△ABA1的面积,最后根据锥体体积公式,得到三棱锥C1-ABA1的体积.
解答:
(I)证明:连接AB1,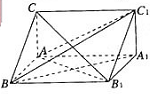
∵ABC-A1B1C1是直三棱柱,
∴平面ABC⊥平面ABB1A1,
又∵平面ABC∩平面ABB1A1=AB,AC⊥AB,
∴AC⊥平面ABB1A1,
∵BA1?平面ABB1A1,∴AC⊥BA1,
∵矩形ABB1A1中,AB=AA1,
∴四边形ABB1A1是正方形,
∴AB1⊥BA1,
又∵AB1、CA是平面ACB1内的相交直线,
∴BA1⊥平面ACB1;
(Ⅱ)解:∵AB=2,BC=
,
∴Rt△ABC中,AC=1
∴直三棱柱ABC-A1B1C1中,A1C1=AC=1
又∵AC∥A1C1,AC⊥平面ABB1A1,
∴A1C1是三棱锥C1-ABA1的高.
∵△ABA1的面积等于正方形ABB1A1面积的一半
∴S△ABA1=
AB2=2
∴三棱锥C1-ABA1的体积为V=
×S△ABA1×A1C1=
.

∵ABC-A1B1C1是直三棱柱,
∴平面ABC⊥平面ABB1A1,
又∵平面ABC∩平面ABB1A1=AB,AC⊥AB,
∴AC⊥平面ABB1A1,
∵BA1?平面ABB1A1,∴AC⊥BA1,
∵矩形ABB1A1中,AB=AA1,
∴四边形ABB1A1是正方形,
∴AB1⊥BA1,
又∵AB1、CA是平面ACB1内的相交直线,
∴BA1⊥平面ACB1;
(Ⅱ)解:∵AB=2,BC=
| 5 |
∴Rt△ABC中,AC=1
∴直三棱柱ABC-A1B1C1中,A1C1=AC=1
又∵AC∥A1C1,AC⊥平面ABB1A1,
∴A1C1是三棱锥C1-ABA1的高.
∵△ABA1的面积等于正方形ABB1A1面积的一半
∴S△ABA1=
| 1 |
| 2 |
∴三棱锥C1-ABA1的体积为V=
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题根据底面为直角三角形的直三棱柱,证明线面垂直并且求三棱锥的体积,着重考查了直线与平面垂直的性质与判定和锥体体积公式等知识点,属于中档题.

练习册系列答案
相关题目
 如图,已知平面四边形ABCP中,D为PA的中点,PA⊥AB,CD∥AB,且PA=CD=2AB=4.将此平面四边形ABCP沿CD折成直二面角P-DC-B,连接PA、PB,设PB中点为E.
如图,已知平面四边形ABCP中,D为PA的中点,PA⊥AB,CD∥AB,且PA=CD=2AB=4.将此平面四边形ABCP沿CD折成直二面角P-DC-B,连接PA、PB,设PB中点为E.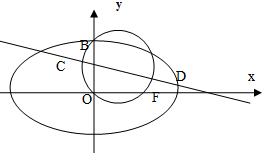 如图,已知圆G:x2+y2-2x-
如图,已知圆G:x2+y2-2x- 如图,在三棱锥S-ABC中,SC⊥平面ABC,M、N分别是SB和SC的中点,设MN=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°
如图,在三棱锥S-ABC中,SC⊥平面ABC,M、N分别是SB和SC的中点,设MN=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60° 如图所示,已知圆C:(x+1)2+y2=8,A(1,0)为定点,B为圆C上的动点,线段AB的垂直平分线交BC于点D,点D的轨迹为曲线E.
如图所示,已知圆C:(x+1)2+y2=8,A(1,0)为定点,B为圆C上的动点,线段AB的垂直平分线交BC于点D,点D的轨迹为曲线E.