题目内容
在平面直角坐标系xOy中,设点F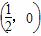 ,直线l:x=-
,直线l:x=-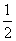 ,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.
,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.
(1)求动点Q的轨迹方程C;
(2)设圆M过A(1,0),且圆心M在曲线C上,TS是圆M在y轴上截得的弦,当M运动时,弦长|TS|是否为定值?请说明理由.
解:(1)依题意知,点R是线段FP的中点,
 且RQ⊥FP,
且RQ⊥FP,
∴RQ是线段FP的垂直平分线.
∵|PQ|是点Q到直线l的距离.
点Q在线段FP的垂直平分线上,
∴|PQ|=|QF|.
故动点Q的轨迹是以F为焦点,l为准线的抛物线,其方程为y2=2x(x>0).
(2)弦长|TS|为定值.理由如下:取曲线C上一点M(x0,y0),M到y轴的距离为d=|x0|=x0,
圆的半径r=|MA|= ,
,
则|TS|= ,
,
因为点M在曲线C上,所以x0= ,
,
所以|TS|=2 =2,是定值.
=2,是定值.

练习册系列答案
相关题目
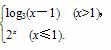 则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为( )
则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为( ) +
+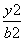 =1(a>b>0)上的一点,若
=1(a>b>0)上的一点,若 ·
· =0,tan∠PF1F2=
=0,tan∠PF1F2=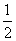 ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )
 D.
D.
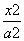 -
-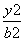 =1(a>0,b>0)上一点,M、N分别是双曲线E的左、右顶点,直线PM,PN的斜率之积为
=1(a>0,b>0)上一点,M、N分别是双曲线E的左、右顶点,直线PM,PN的斜率之积为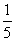 .
. =λ
=λ +
+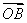 ,求λ的值.
,求λ的值. 中,已知
中,已知 ,
, ,则
,则 。
。 (
( ),数列
),数列 项的和记为
项的和记为 ,则
,则 。
。 的前
的前 项和
项和 ,那么它的通项公式是
,那么它的通项公式是  B.
B. C.
C. D.
D.