题目内容
3.当x,y满足条件$\left\{\begin{array}{l}{x≤y}\\{x≥0}\\{2x+y-3≤0}\end{array}\right.$时,目标函数z=3x+2y的最大值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,通过图象平移确定目标 函数的最大值
解答 解:由z=3x+2y,得y=-$\frac{3}{2}$x+$\frac{z}{2}$,作出不等式对应的可行域,如图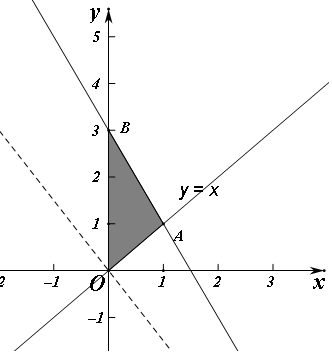
平移直线y=-$\frac{3}{2}$x+$\frac{z}{2}$,由平移可知当直线y=-$\frac{3}{2}$x+$\frac{z}{2}$经过点B(0,3)时,
直线y=-$\frac{3}{2}$x+$\frac{z}{2}$的截距最大,此时z取得最大值为3×0+2×3=6,
即目标函数z=x+3y的最大值为6.
故选:D
点评 本题主要考查线性规划的应用,利用图象平行求得目标函数的最大值和最小值,数形结合是解决线性规划问题中的基本方法.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
11.已知抛物线y2=2px(p>0)上的点A到焦点F距离为4,若在y轴上存点B(0,2)使得$\overrightarrow{BA}$$•\overrightarrow{BF}$=0,则该抛物线的方程为( )
| A. | y2=8x | B. | y2=6x | C. | y2=4x | D. | y2=2x |
18.设抛物线C:y2=2px(p>0)的焦点F,其准线与x轴相交于点Q,过点F倾斜角为锐角θ的直线交抛物线于A,B两点,若∠QBF=90°,则cosθ=$\frac{\sqrt{5}-1}{2}$.
8.关于x的方程($\frac{1}{3}$)|x|+a-1=0有解,则a的取值范围是( )
| A. | 0≤a<1 | B. | -1<a≤0 | C. | a≥1 | D. | a>0 |
15.已知正三棱锥P-ABC的底面ABC的边长为a,高为h,在正三棱锥内任取一点M,使得VP-ABC>2VM-ABC的概率是( )
| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
12.函数f(x)=x2-x-2(-5≤x≤5),在其定义域内任取一点x0,使f(x0)<0的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{10}$ | D. | $\frac{4}{5}$ |