题目内容
19.以(1,1)和(2,-2)为一条直径的两个端点的圆的方程为x2+y2-3x+y=0.分析 以(1,1)和(2,-2)为直径的圆的圆心与半径,即可求解圆的方程.
解答 解:以(1,1)和(2,-2)为直径的圆的圆心为($\frac{3}{2}$,-$\frac{1}{2}$),
半径为:r=$\frac{1}{2}$$\sqrt{(2-1)^{2}+({-2-1)}^{2}}$=$\frac{\sqrt{10}}{2}$.
∴圆的方程为(x-$\frac{3}{2}$)2+(x+$\frac{1}{2}$)2=$\frac{10}{4}$,
整理,得x2+y2-3x+y=0.
故答案为:x2+y2-3x+y=0.
点评 本题考查圆的标准方程的求法,解题时要认真审题,注意圆的方程的合理运用.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
9.R表示实数集,集合M={x|0<x<2},N={x|x2+x-6≤0},则下列结论正确的是( )
| A. | M∈N | B. | ∁RM⊆N | C. | M∈∁RN | D. | ∁RN⊆∁RM |
10.在△ABC中,如果sinA:sinB:sinC=6:7:9,则△ABC一定是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 不能确定 |
7.在数列{an}中,a1=1,且anan+1+$\sqrt{3}$(an-an+1)+1=0,则a2016=( )
| A. | 1 | B. | -1 | C. | 2+$\sqrt{3}$ | D. | 2-$\sqrt{3}$ |
 如图,在平行四边形ABCD中,已知$\overrightarrow{|AB|}$=8,$\overrightarrow{|AD|}$=5,$\overrightarrow{CP}=3\overrightarrow{PD}$,$\overrightarrow{AP}•\overrightarrow{BP}=2$,则$\overrightarrow{AB}•\overrightarrow{AD}$=22.
如图,在平行四边形ABCD中,已知$\overrightarrow{|AB|}$=8,$\overrightarrow{|AD|}$=5,$\overrightarrow{CP}=3\overrightarrow{PD}$,$\overrightarrow{AP}•\overrightarrow{BP}=2$,则$\overrightarrow{AB}•\overrightarrow{AD}$=22.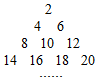 将正偶数排列如图,其中第i行和第j列的数表示为aij=(i,j∈N+),例如a43=18,若aij=2016,则i+j=63.
将正偶数排列如图,其中第i行和第j列的数表示为aij=(i,j∈N+),例如a43=18,若aij=2016,则i+j=63.